Ch9 Part2
Ch9 Part2
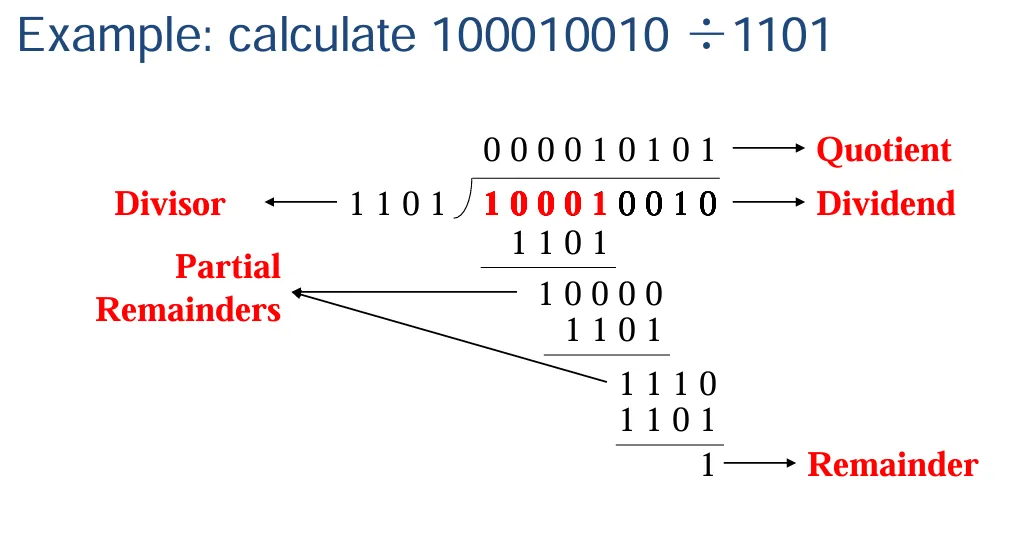
Integer Division
Manual Division of Positive Integers(人工正整数除法)
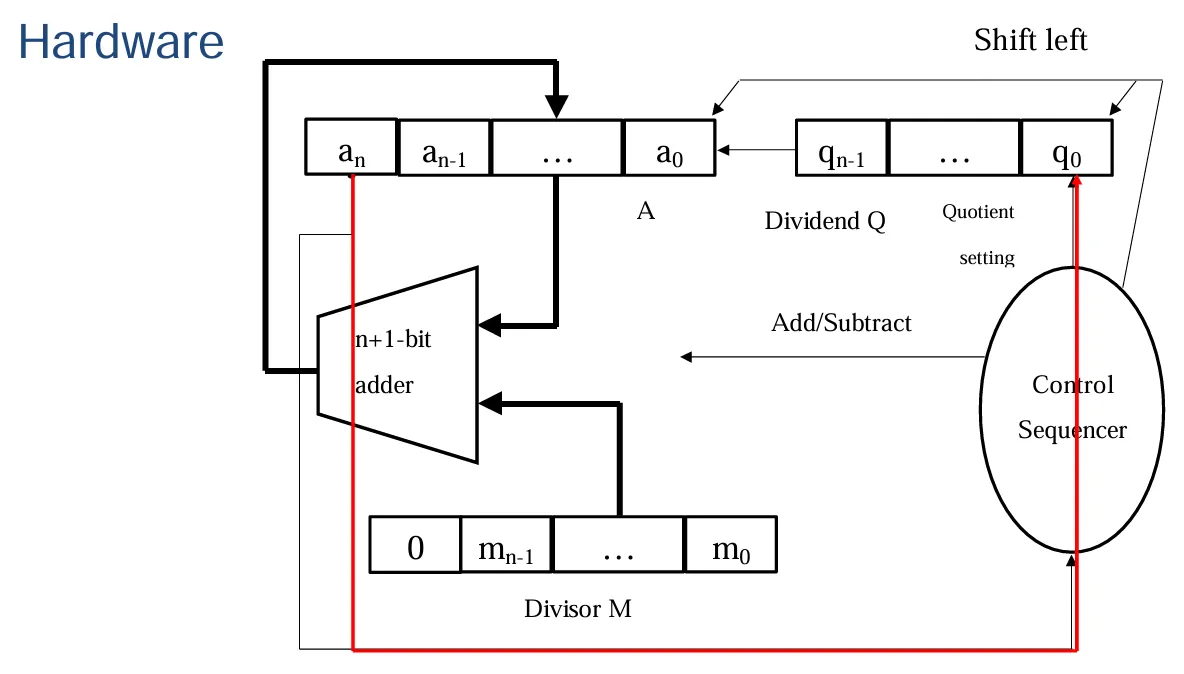
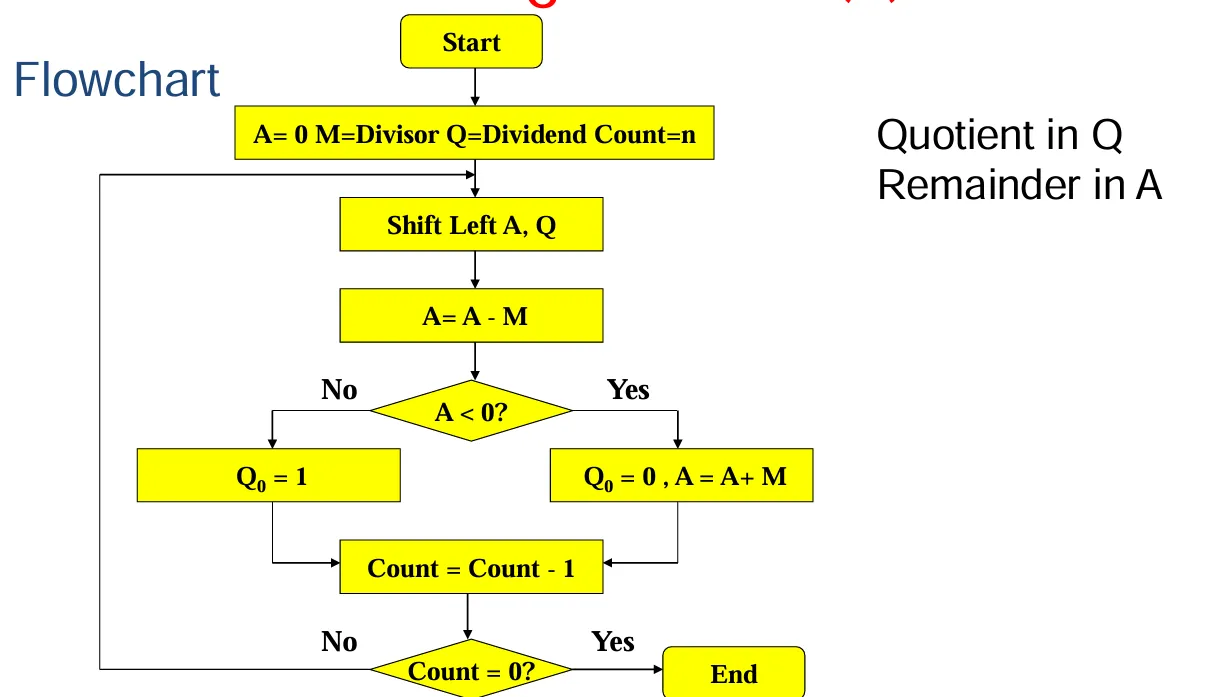
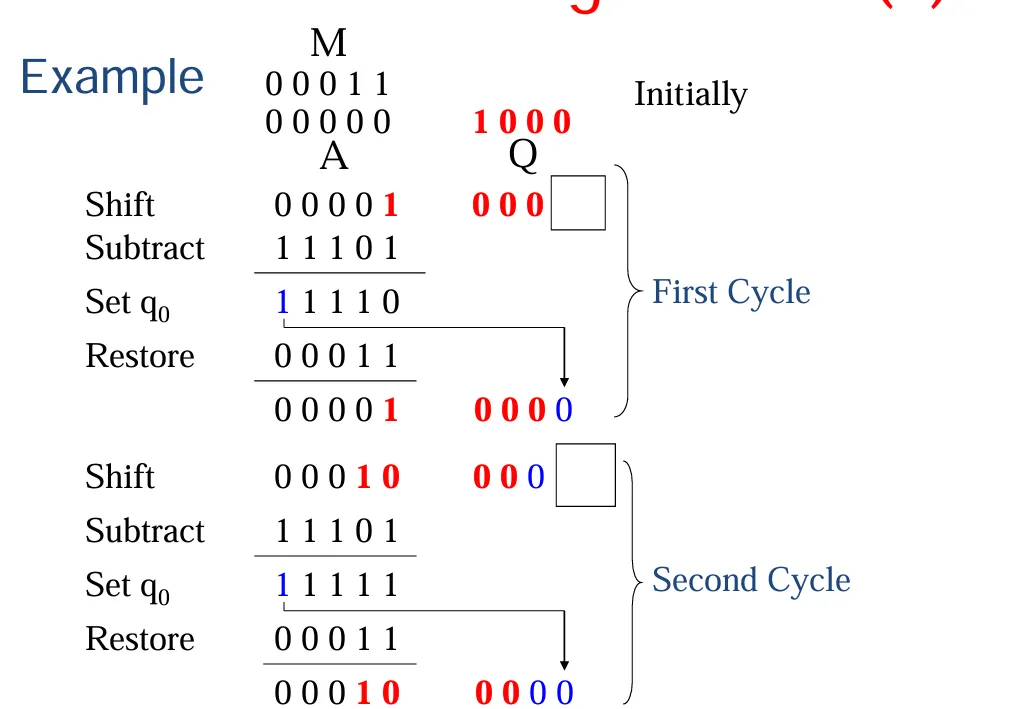
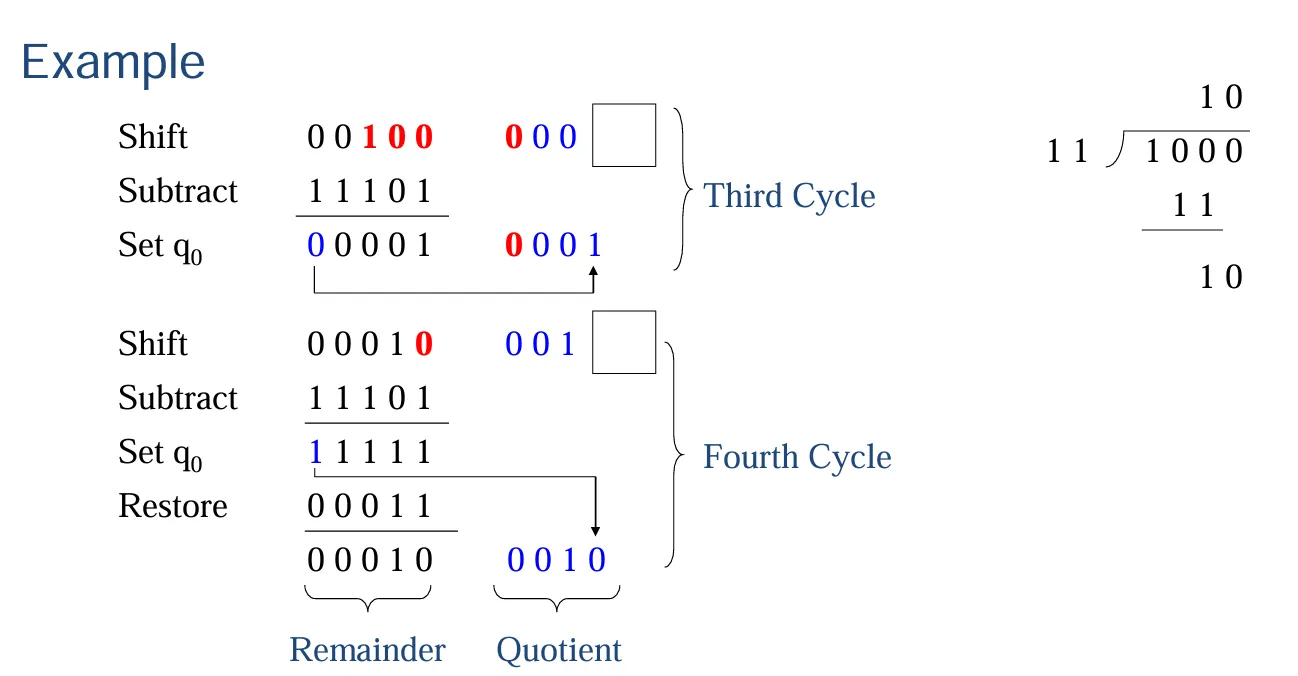
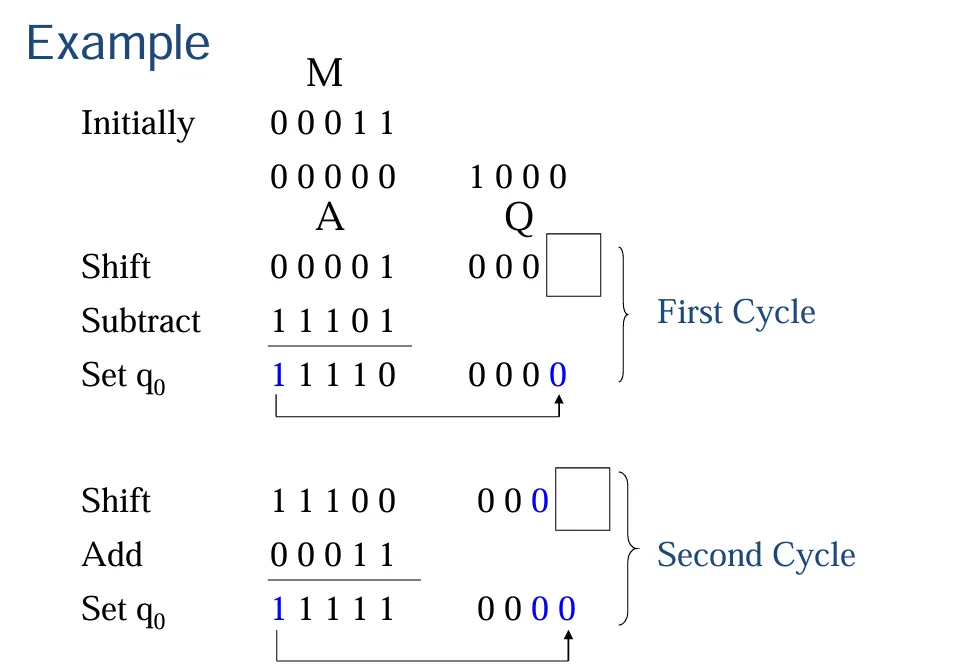
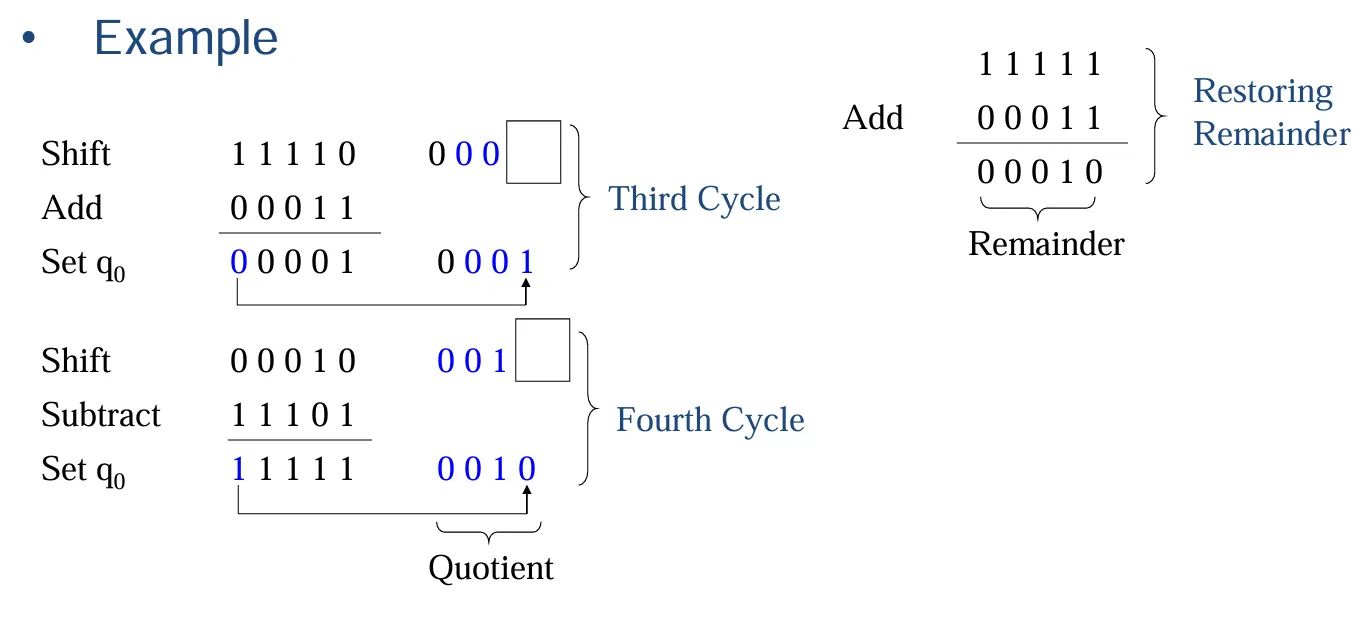
恢复除法
一个实际计算的例子:
不恢复除法
结论
- 与乘法算法的对比:对于有符号操作数,没有像有符号乘法算法那样简单直接的除法算法。这表明在运算算法的简洁性方面,除法与乘法存在差异,除法运算的算法可能会更复杂一些。
- 操作数处理方式:在进行除法运算时,可以先对操作数进行处理,将它们转换为正值。这种预处理方式有助于简化后续的除法运算步骤,因为在正数范围内进行除法运算可能会更容易处理。
- 结果转换:在使用恢复除法(restoring division)或者不恢复除法(non - restoring division)等算法完成除法运算之后,需要根据实际情况将结果转换为正确的有符号数值。这一步骤是为了确保最终得到的结果符合有符号数除法运算的要求,保证结果的准确性和正确性。
Floating-point Numbers & IEEE 754 Standard
数的格式概述
根据二进制小数点位置是否固定,存在两种数的格式:
- 定点数:例如整数,其隐含的二进制小数点位于数的最右端。
- 浮点数。
定点表示
- 定点记数法定义:定点记数法表示的数,其二进制小数点右边的位数是固定不变的。
- 不同类型定点数示例:
- 无符号整数:二进制小数点右边没有位数。
- 有符号整数:同样二进制小数点位于最右端,右边无位数。
- 有符号分数:二进制小数点位于符号位的右边。
设\(X = x_n\cdots x_0\)为定点数
- 若\(X\)是整数:
- 二进制小数点位置:位于\(x_0\)的右边。
- 取值范围:\(-2^n \leq V(X) \leq 2^n - 1\)。
- 若\(X\)是纯分数:
- 二进制小数点位置:在\(x_n\)和\(x_{n - 1}\)之间。
- 取值范围:\(-1 \leq V(X) \leq 1 - 2^{-n}\)。
定点数表示的局限性
- 大小数表示局限:非常大的整数以及非常小的分数都无法用定点数来表示。
- 示例说明:
- 32 位有符号定点格式可表示的值域(整数情况):其取值范围是\(-2^{31} \leq V(X) \leq 2^{31} - 1\)。
- 32 位有符号定点格式可表示的值域(分数情况):取值范围是\(-2^{-31} \leq V(X) \leq 1 - 2^{-31}\),具体区间为\([-4.55\times10^{10}, 4.55\times10^{10}]\)(这里原内容区间表示不太规范,推测大致如此)。
- 科学计算中的示例体现局限:像在科学计算里,阿伏伽德罗常数\(6.02214076×10^{23} mol^{-1} = 0.602214076×10^{24} mol^{-1}\)以及普朗克常数\(6.62607015×10^{-34}J\cdot s = 0.62607015×10^{-33}J\cdot s\)这样数值巨大或极小的数据,用定点数格式很难准确表示,凸显出定点数在表示这类科学计算中常见数据时的不足。
浮点表示
- 浮点表示的特点:在浮点表示中,二进制小数点的位置是可变的,并且会随着计算的进行自动调整。同时,在浮点表示里必须明确给出二进制小数点的位置,其形式与科学记数法类似。
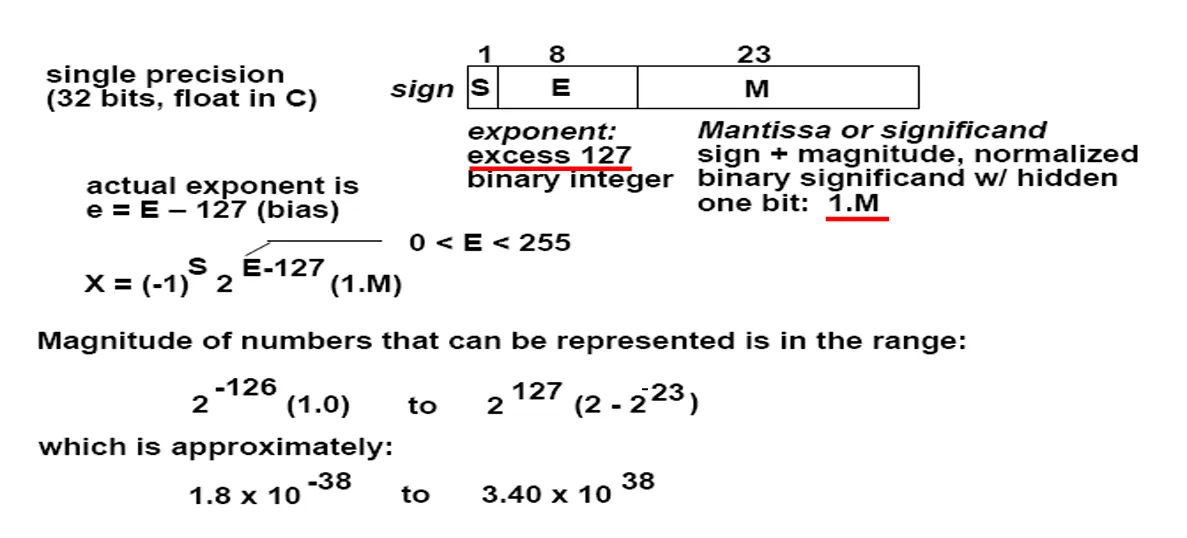
数值形式
- 各部分构成及含义:
- 符号位(S):符号位\(S\)用于确定该数是正数还是负数。
- 尾数(M):尾数\(M\)是采用原码或者补码表示的分数形式,它包含了有效数字部分。
- 指数(E):指数\(E\)采用补码或者偏移(biased)记数法来表示底数的幂次,但它并非实际的指数,实际指数用\(e\)来表示。
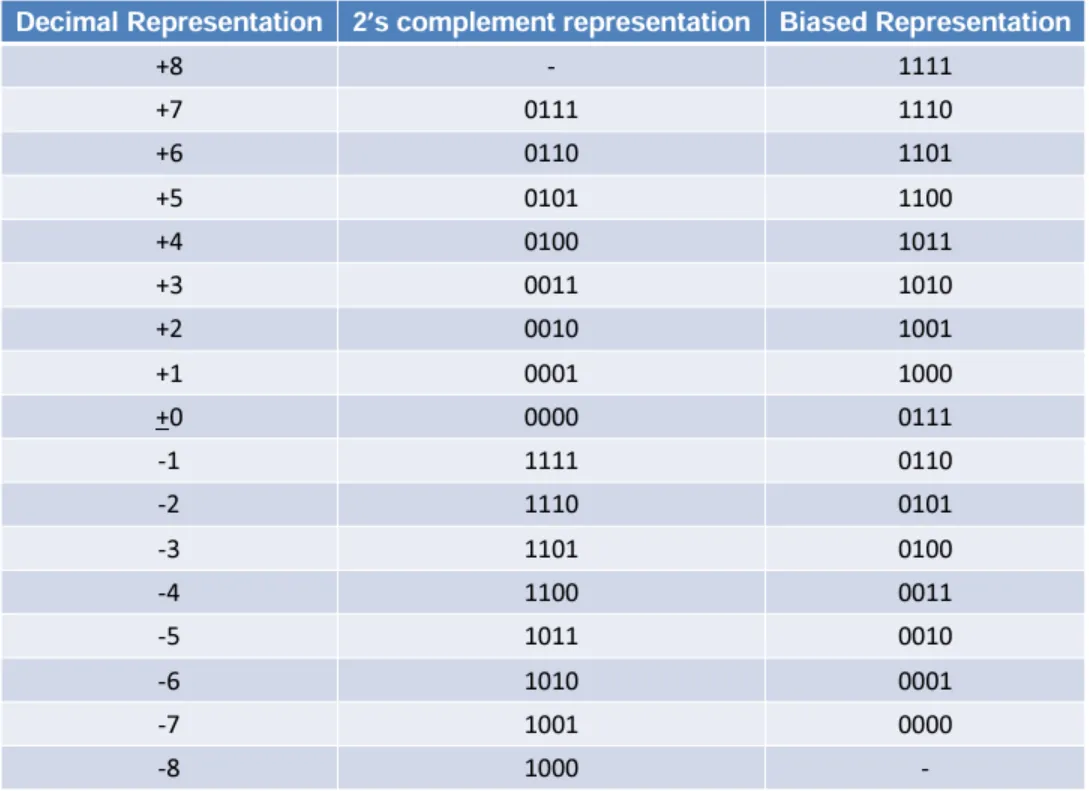
偏移(Excess 或 Biased)记数法
- 采用原因及计算方式:由于采用补码表示的负指数看起来像是一个很大的指数,所以采用偏移记数法,即从指数字段中减去一个固定值来得到真实的指数,其计算公式为\(E = e + (2^{k - 1} - 1)\),这里\(e\)是实际指数,\(k\)是指数部分的位数。
- 重要特性:需要注意的是,当把偏移表示的各位当作无符号整数看待时,数之间的相对大小关系并不会改变。
规范化(Normalization)
- 规范化定义及示例:按照惯例,把小数点放置在第一个(非零)有效数字右边的数称为规范化的数,例如\(1.0×10^{-9}(ok)\)、\(0.1×10^{-10}(wrong)\)(这是规范化的科学记数法示例)等。在规范化的二进制表示中,尾数的最高有效位总是等于\(1\),例如\(\pm0.1bbb\cdots b×2^{E}\)(其中\(b\)为\(0\)或\(1\)),像\(0.0110×2^{6}\)就不是规范化的,而\(0.110×2^{5}\)是规范化的。
IEEE 754 标准
- 制定主体:由电气与电子工程师协会(Institute of Electrical and Electronics Engineers)制定。
- 地位与作用:是表示浮点数最为常用的标准。它于 1985 年确立,旨在作为浮点算术运算的统一标准,其制定目的是方便程序在不同处理器之间的可移植性,并且鼓励开发复杂的、面向数值计算的程序,目前得到了所有主流 CPU 的支持。
单精度浮点数格式与双精度浮点数格式
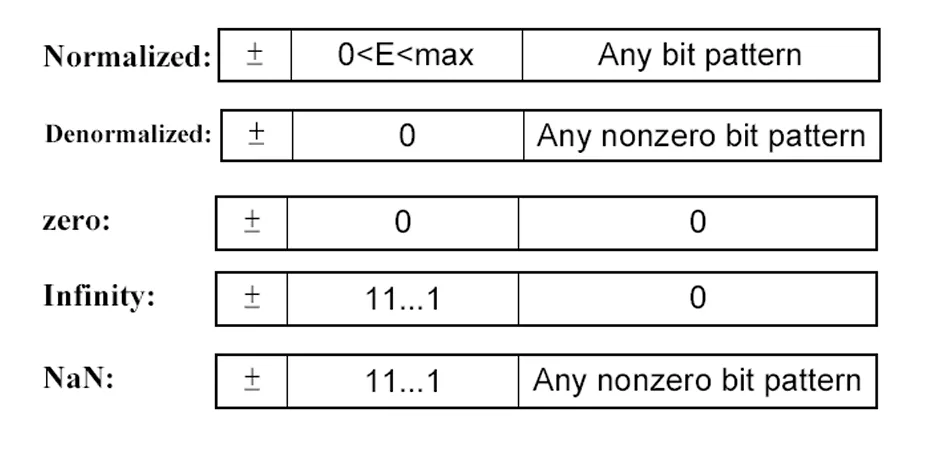
特殊值相关情况
- 零(Zero):
- 表示形式及值:当符号位\(S = 0\)或\(1\),指数位\(E = 0\),尾数位\(M = 0\)(即\(0.M\)形式)时,表示的值为\(\pm 0\)。指数域为零是一种特殊情况,意味着尾数不存在隐含的最高位\(1\)。
- 无穷大(Infinity):
- 产生情况及表示形式、值:在发生溢出的运算操作时会出现,例如\(1.0 / 0.0\)的结果就是\(+\infty\)。其表示形式为符号位\(S = 0\)或\(1\),指数位\(E = 255\)(单精度时)或\(2047\)(双精度时),尾数位\(M = 0\),对应的数值就是\(\pm\infty\)。
- 非数(NaN,Not a Number):
- 代表情况及表示形式、值:用于表示无法确定数值的情况,比如对\(-1\)求平方根(\(\sqrt{-1}\))这样的操作结果就用\(NaN\)表示。其表示形式为符号位\(S = 0\)或\(1\),指数位\(E = 255\)(单精度时)或\(2047\)(双精度时),尾数位\(M \neq 0\),其值就是\(NaN\)。
- 非规格化数(Denormal Numbers):
- 特点及相关设定:这类数在二进制小数点左边不存在隐含的\(1\),所有非规格化数都假定其指数域的偏移值为\(1\),它们是非常接近\(0.0\)的数,并且无法进行规范化操作,零实际上也可看作是一种特殊的非规格化数。其精度会随着数值变小而降低,存在“渐进下溢”现象,其表示形式为符号位\(S = 0\)或\(1\),指数位\(E = 0\),尾数位\(M \neq 0\),对应的值为\(\pm 0.M×2^{-126}\)(单精度时)或\(\pm 0.M×2^{-1022}\)(双精度时)。
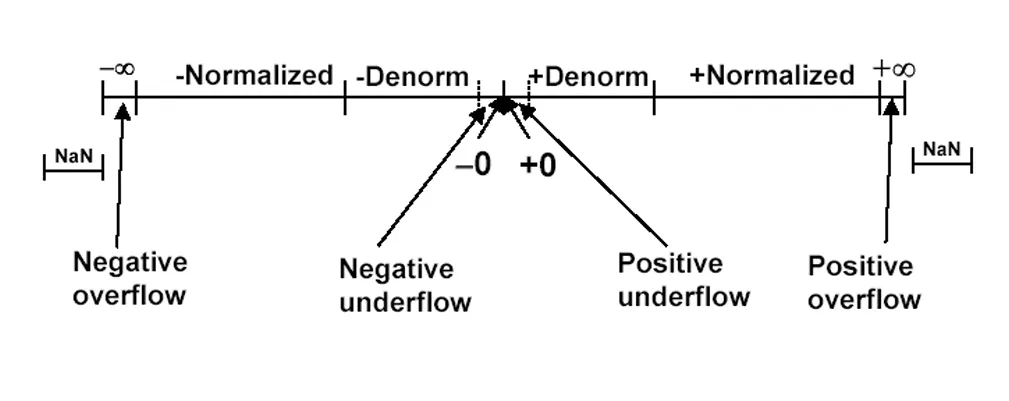
特殊值总结
总结部分
- 基本要求:一台计算机若要符合 IEEE 标准,至少要提供单精度表示形式,双精度表示则是可选的。
- 扩展精度格式作用:扩展单精度(位数超过 32 位)和扩展双精度(位数超过 64 位)格式有助于减小一系列计算中累积的舍入误差大小,能够提升诸如正弦、余弦等基本函数求值的准确性。
- 精度与范围的权衡:增大尾数的大小可以提高精度,而增加指数部分的大小则能够扩大数值的表示范围,在实际应用中需要根据具体需求在这两方面进行权衡考虑。
对齐(Alignment)
- 在浮点运算中的地位及含义:对齐是浮点数进行加法和减法运算的首要步骤。其具体操作是在进行加/减法之前,如果参与运算的两个浮点数的指数不同,就需要对这两个操作数进行调整,使得它们的指数相等。
- 示例说明(十进制情况):例如进行十进制加法运算\((123×10^0)+(456×10^{-2})\),实现对齐的方式有两种,一种是\((123×10^0)+(456×10^{-2}) = (123×10^0)+(4.56×10^0)\),也就是将第二个数的尾数的数值部分右移 1 位,同时指数递增,直至两个数的指数相等;另一种是\((123×10^0)+(456×10^{-2}) = (12300×10^{-2})+(456×10^{-2})\),同样是通过对尾数部分进行移位以及调整指数来达到指数相等的目的。
加/减运算规则(针对 IEEE 单精度浮点数)
- 步骤一:选择指数较小的那个数,将其尾数向右移位,移位的步数等于两个数指数的差值。
- 步骤二:把运算结果的指数设置为两个数中较大的那个指数值。
- 步骤三:对两个数的尾数进行加/减法运算,并确定结果的符号。
- 步骤四:如果有必要,对得到的结果进行规范化处理,使其符合浮点数的规范表示形式。
乘法运算规则(针对 IEEE 单精度浮点数)
- 步骤一:将两个数的指数相加,然后减去 127(这与 IEEE 单精度浮点数中指数的偏移表示相关)。
- 步骤二:把两个数的尾数相乘,并确定结果的符号。
- 步骤三:如有需要,对相乘得到的结果进行规范化处理。
除法运算规则(针对 IEEE 单精度浮点数)
- 步骤一:用被除数的指数减去除数的指数,然后加上 127。
- 步骤二:将被除数的尾数除以除数的尾数,并确定结果的符号。
- 步骤三:必要时,对相除得到的结果进行规范化处理,确保其符合浮点数的表示规范。
浮点运算中需考虑的问题(1)——保护位(Guard Bits)
- 作用:为提高浮点计算的精度,会使用保护位。尾数中额外保留的那些位就被称作保护位,它们用于在尾数的右端用 0 进行填充。
- 重要性:在中间运算步骤中保留保护位很重要,这样能使最终结果达到最高的精度。
浮点运算中需考虑的问题(2)——保护位(续)
- 示例:设\(X =
1.00\cdots00×2^1\),\(Y =
1.11\cdots11×2^0\)(\(X\)和\(Y\)均为 IEEE 单精度格式),计算\(Z = X - Y\)。
- 无保护位时:\(X = 1.000\cdots00×2^1\),\(Y\)需调整为\(0.111\cdots11×2^1\),则\(Z = 0.000\cdots01×2^1=1.000\cdots00×2^{-22}\)。
- 有保护位时:\(X = 1.000\cdots00\ 0 ×2^1\),\(Y = 0.111\cdots11\ 1×2^1\),\(Z = 0.000\cdots00\ 1×2^1 = 1.000\cdots00\ 0×2^{-23}\),展示了保护位对结果精度的影响。
浮点运算中需考虑的问题(3)——截断(Truncation)
- 尾数长度限制及截断需求:尾数有特定的长度限制(单精度为 23 位,双精度为 52 位),而算术运算可能产生精度更高的尾数,在存储浮点数之前,多余的位就需要被丢弃,这一过程就是截断。
- 截断方法要求:截断方法应是无偏的,即误差能相互补偿。常见的截断方法有砍截(Chopping)、冯·诺依曼舍入(Von Neumann Rounding)、常规舍入(Rounding)等。
浮点运算中需考虑的问题(4)——砍截(Chopping)
- 操作方式:直接去掉保护位,对保留的位不做任何改变,这种方法易于实现。
- 偏差情况及误差范围:但它是有偏的,因为所有数值都会朝着尾数更小的值进行舍入。其误差范围在保留位的最低有效位上是从 0 到接近 1,不是最优的截断方法。
- 示例:比如将\(0.b_{-1}b_{-2}b_{-3}010\)截断为三位,就变为\(0.b_{-1}b_{-2}b_{-3}\),实际上从\(0.b_{-1}b_{-2}b_{-3}000\)到\(0.b_{-1}b_{-2}b_{-3}111\)这个范围内的所有分数都会被截断为\(0.b_{-1}b_{-2}b_{-3}\),在这个三位结果中的误差范围是从 0 到\(0.000111\)。
浮点运算中需考虑的问题(5)——冯·诺依曼舍入(Von Neumann Rounding)
- 舍入规则:区分精确表示和向相邻奇数边界舍入这两种情况。一是如果要去除的位全是 0,则直接舍去,保留的位不做改变;二是如果要去除的位中有 1,则将保留位的最低有效位置为 1。
- 实现难度与偏差情况、误差范围:这种方法仍然比较容易实现,并且是无偏的,舍入在正负值方向上是均匀分布的,其误差范围在保留位的最低有效位上处于\(-1\)到\(+1\)之间,比砍截方法好,但存在较高的绝对误差。
- 示例:将\(0.b_{-1}b_{-2}b_{-3}000 - 0.b_{-1}b_{-2}b_{-3}111\)截断为三位时,\(0.b_{-1}b_{-2}b_{-3}000\Rightarrow 0.b_{-1}b_{-2}b_{-3}\),而\(0.b_{-1}b_{-2}b_{-3}001 - 0.b_{-1}b_{-2}b_{-3}111\Rightarrow 0.b_{-1}b_{-2}1\)。
浮点运算中需考虑的问题(6)——常规舍入(Rounding)
舍入规则:根据要截断的尾数部分的最高有效位等情况区分三种情形进行舍入。一是如果要截断的尾数部分的最高有效位是 0,则执行砍截操作;二是如果要截断的尾数部分的最高有效位是 1,且其他要截断的位中有 1,则在保留的最低有效位上加 1;三是如果要截断的尾数部分的最高有效位是 1,且其他要截断的位都是 0,当保留的最低有效位是 0 时执行砍截,是 1 时在最低有效位上加 1。
实现难度与偏差情况、误差范围:实现起来需要花费一些功夫,但它是无偏的,舍入在正负值方向上是均匀分布的,其误差范围在保留位的最低有效位上处于\(-\frac{1}{2}\)到\(+\frac{1}{2}\)之间。
示例:将\(0.b_{-1}b_{-2}b_{-3}000 - 0.b_{-1}b_{-2}b_{-3}111\)截断为三位时,不同情况按相应规则进行舍入操作,如\(0.b_{-1}b_{-2}b_{-3}000 - 0.b_{-1}b_{-2}b_{-3}011\Rightarrow 0.b_{-1}b_{-2}b_{-3}\)等。并且常规舍入是 IEEE 浮点标准中指定的默认截断模式。
\(0.b_{-1}b_{-2}b_{-3}101 - 0.b_{-1}b_{-2}b_{-3}111\Rightarrow 0.b_{-1}b_{-2}b_{-3}+0.001\)
\(0.b_{-1}b_{-2}b_{-3}100 - 0.b_{-1}b_{-2}0100\Rightarrow 0.b_{-1}b_{-2}0\)
\(0.b_{-1}b_{-2}b_{-3}100 - 0.b_{-1}b_{-2}1100\Rightarrow 0.b_{-1}b_{-2}1+0.001\)
浮点运算中需考虑的问题(7)——规范化(Normalization)
- IEEE 单精度规范化浮点数要求:指数部分\(E\neq000\cdots0\)(8 位)且\(E\neq111\cdots1\)(8 位),\(E\)采用偏移值编码,规范化的有效数字形式为\(1.M\)。如果一个数是非规范化的,总能通过对尾数进行移位以及调整指数的方式将其转化为规范化形式。
浮点运算中需考虑的问题(8)——溢出(Overflow)
- 总体概念:在计算过程中,可能会产生超出正常可表示范围的数,这就涉及到溢出情况,包括指数溢出和尾数溢出等不同类型。
- 指数溢出:
- 正指数溢出情况:当正指数超过了最大可能的指数值时发生,例如在 IEEE 单精度中,\(e > 127\),在一些系统中,这种情况可能会被指定为正无穷或负无穷。
- 负指数溢出情况(指数下溢):当负指数小于最小可能的指数值时发生,例如在 IEEE 单精度中,\(e < -126\),意味着这个数太小以至于无法表示,可能会被报告为 0。
- 尾数溢出:
- 同号尾数相加溢出情况:两个同号尾数相加时,可能会产生从最高有效位进位的情况,此时需要将结果的尾数右移,并递增指数。
- 尾数下溢情况:在对尾数进行对齐操作时,数位可能会从尾数的右端流出,这可以通过使用保护位以及某种截断方法来解决。
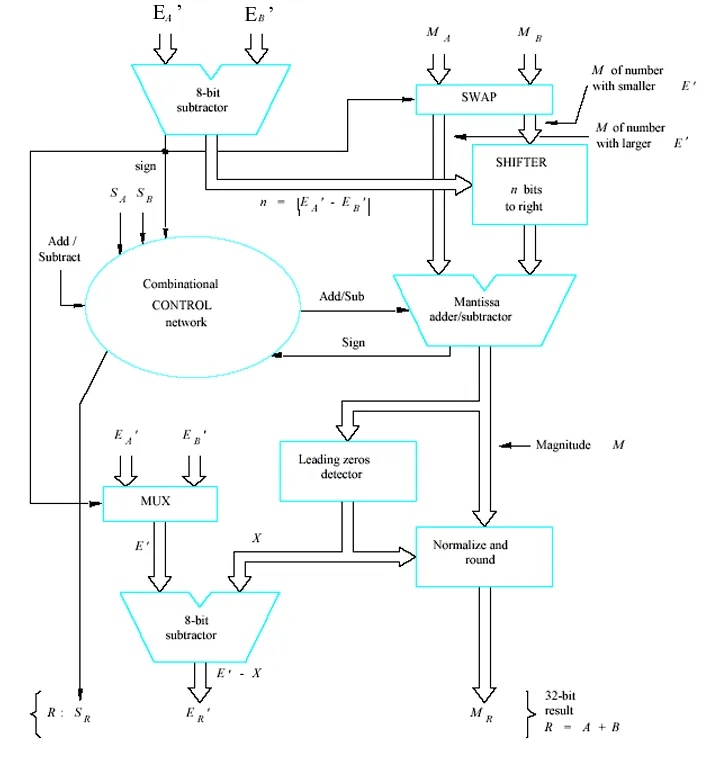
浮点运算中需考虑的问题(9)——实现浮点运算的方法
- 软件例程与硬件例程:实现浮点运算有软件例程和硬件例程这两种方式。计算机通常会为浮点运算提供机器指令来支持运算操作。
- 注意事项:无论是哪种情况,计算机都必须能够在用户输入输出的十进制数表示和内部运算使用的格式之间进行转换。
- 硬件实现示例:例如对于 32 位操作数,以\(\{A: S_A, E_A’, M_A\}\),\(\{B: S_B, E_B’, M_B\}\)这样的形式来表示参与运算的数(这里\(S\)表示符号位,\(E\)表示指数相关部分,\(M\)表示尾数部分),不同的实现方式会基于这样的操作数表示来完成具体的浮点运算过程。