DIS03AB
DIS03AB
1. 图论基础
对于每种类型的图,选择该图类型满足的所有属性。
- 平面图。设\(v\)、\(e\)、\(f\)分别为顶点数、边数和面数。
- \(i. v + f = e + 2\)
- \(ii. e\leq2v - 4\)
- $iii. $任何平面图最多可以用 5 种颜色进行顶点着色。
- 树
- \(i.\) 有\(\vert V\vert - 1\)条边
- $ii. $可以有环
- $iii. $添加一条边会减少连通分量的数量
- 超立方体。设\(n\)为超立方体的维度。
- \(i. \vert V\vert = 2^n\)
- \(ii. \vert E\vert = n\cdot2^{n - 1}\)
解决方案:
- 仅 iii。对于\(i\),欧拉公式要求图是连通的,所以对于不连通的平面图该公式不成立。对于\(ii\),当平面图是二分图时该式成立。注意对于\(iii\),实际上最多可以用 4 种颜色完成。
- 仅 i。对于\(ii\),树总是无环的。对于\(iii\),向树中添加一条边不会减少连通分量的数量,因为树是连通图,即连通分量的数量为 1。
- \(i\)、\(ii\)。\(ii\)可以根据握手引理推导出来,因为在\(n\)维超立方体中有\(2^n\)个顶点,并且每个顶点的度数为\(n\),因此,\(\vert E\vert=\frac{n\cdot2^n}{2}=n\cdot2^{n - 1}\)。
2. 总是、有时或从不
在下面的每个部分中,你将获得关于图\(G\)的一些信息。仅使用当前部分中的信息,说明\(G\)总是平面图、总是非平面图还是两者皆有可能。如果你认为它总是平面图或总是非平面图,请证明它。如果你认为两者皆有可能,请给出一个平面图示例和一个非平面图示例。
- \(G\)可以用 4 种颜色进行顶点着色。
- \(G\)需要 7 种颜色进行顶点着色。
- \(e\leq3v - 6\),其中\(e\)是\(G\)的边数,\(v\)是\(G\)的顶点数。
- \(G\)是连通的,并且\(G\)中的每个顶点的度数最多为 2。
- \(G\)中的每个顶点的度数最多为 2。
解决方案:
- 两者皆有可能。根据四色定理,任何平面图都可以提供平面图示例。最简单的非平面图示例是\(K_{3,3}\),它可以用 2 种颜色着色,因为它是二分图。(当然,任何可以用仅 2 种颜色着色的图也可以用 4 种颜色着色。)
- 总是非平面图。四色定理告诉我们,如果一个图是平面图,它可以只用 4 种颜色着色。其逆否命题是,如果一个图需要超过 4 种颜色进行顶点着色,它一定是非平面图。(使用五色定理或六色定理也可以。)
- 两者皆有可能。从笔记中我们知道每个平面图都遵循这个公式,所以任何平面图都是有效的平面图示例。最简单的非平面图示例仍然是\(K_{3,3}\),它有\(e = 9\)和\(v = 6\),这意味着我们的公式变为\(9\leq3(6)-6 = 12\),这当然是正确的。
- 总是平面图。这里有两种情况需要处理:要么\(G\)是一棵树,要么\(G\)不是一棵树,因此包含至少一个环。在前一种情况下,我们立即完成,因为所有树都是平面图。在后一种情况下,考虑\(G\)中的任何一个环。我们知道该环中的每个顶点都与环中其左侧的顶点和右侧的顶点相邻。但我们也知道没有顶点可以连接到超过两个其他顶点,所以该环不与其他任何东西相连。但\(G\)是一个连通图,所以我们必须有\(G\)只是一个大的环。并且我们当然可以在平面上绘制一个简单的环而不交叉任何边,所以即使在这种情况下\(G\)仍然是平面图。 或者,我们可以使用库拉托夫斯基定理;由于每个顶点的度数最多为 2,\(G\)不可能包含\(K_5\)或\(K_{3,3}\)。这意味着\(G\)必须是平面图。
- 总是平面图。\(G\)的每个连通分量都是连通的并且没有度数超过 2 的顶点,所以根据上一部分,它们每个都必须是平面图。因此,\(G\)的每个连通分量都必须是平面图,所以\(G\)本身必须是平面图。 或者,我们可以遵循与上一个替代解决方案相同的过程;每个顶点的度数仍然最多为 2,所以\(G\)不可能包含\(K_5\)或\(K_{3,3}\)。这意味着\(G\)必须是平面图。
3. 图着色
证明最大度数最多为\(k\)的图是\((k + 1)\)可着色的。
解决方案:
尝试证明这个定理的自然方法是对图的最大度数\(k\)使用归纳法。不幸的是,这种方法极其困难,因为当最大度数变化时涵盖所有可能类型的图需要非常小心。在写证明时,你可能会想象某个特定的图,但你的论证可能无法推广。在图论中,归纳参数的典型好选择是\(n\)(节点数)或\(e\)(边数)。我们通常避免对度数进行归纳。 我们对图中的顶点数\(n\)使用归纳法。设\(P(n)\)为命题:最大度数最多为\(k\)的\(n\)个顶点的图是\((k + 1)\)可着色的。
基础情形\(n = 1\):一个 1 个顶点的图最大度数为 0 并且是 1 可着色的,所以\(P(1)\)为真。
归纳步骤:现在假设\(P(n)\)为真,并且让\(G\)是一个\((n + 1)\)个顶点且最大度数最多为\(k\)的图。移除一个顶点\(v\)(以及所有与它相关联的边),留下一个\(n\)个顶点的子图\(H\)。\(H\)的最大度数最多为\(k\),并且根据我们的假设\(P(n)\),\(H\)是\((k + 1)\)可着色的。现在添加回顶点\(v\)。我们可以给\(v\)分配一种颜色(从\(k + 1\)种颜色的集合中),该颜色不同于所有与其相邻的顶点的颜色,因为最多有\(k\)个顶点与\(v\)相邻,所以\(k + 1\)种颜色中至少有一种仍然可用。因此,\(G\)是\((k + 1)\)可着色的。这完成了归纳步骤,定理通过归纳法得证。
4. 超立方体
\(n\)维超立方体\(G=(V,E)\)的顶点集由\(V = \{0,1\}^n\)给出(回想一下,\(\{0,1\}^n\)表示所有\(n\)位字符串的集合)。两个顶点\(x\)和\(y\)之间有一条边当且仅当\(x\)和\(y\)恰好有一位不同。
- 绘制 1 维、2 维和 3 维超立方体,并使用相应的位字符串标记顶点。
- 证明\(n\)维超立方体的边可以用\(n\)种颜色着色,使得没有共享公共顶点的两条边具有相同的颜色。
- 证明对于任何\(n\geq1\),\(n\)维超立方体是二分图。
解决方案:
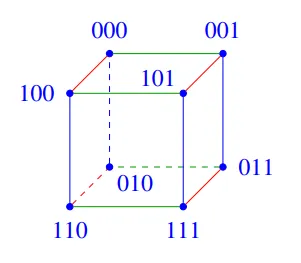
- 这三个超立方体分别是一条线、一个正方形和一个立方体。也可以在注意事项 5 中查看图片。
- 考虑改变第\(i\)位(对于某个\(i\leq
n\))的每条边。每个顶点恰好接触这些边中的一条,因为在任何位串中改变第\(i\)位只有一种方法。将这些边中的每条都着色为颜色\(i\),确保每个顶点将与\(n\)条不同颜色的边相邻,因为有\(n\)个不同的位可以改变,并且表示在不同位上的位变化的两条边没有相同的颜色。
一个三维情况的示例如下(红色是第一位,蓝色是第二位,绿色是第三位):
- 考虑改变第\(i\)位(对于某个\(i\leq
n\))的每条边。每个顶点恰好接触这些边中的一条,因为在任何位串中改变第\(i\)位只有一种方法。将这些边中的每条都着色为颜色\(i\),确保每个顶点将与\(n\)条不同颜色的边相邻,因为有\(n\)个不同的位可以改变,并且表示在不同位上的位变化的两条边没有相同的颜色。
一个三维情况的示例如下(红色是第一位,蓝色是第二位,绿色是第三位):
替代解决方案(使用归纳法):
在\(n = 1\)的基础情形中,只有一条线的超立方体可以用 1 种颜色进行边着色。接下来,假设\(n\)维超立方体可以用\(n\)种颜色着色。回想一下,\((n + 1)\)维超立方体由两个\(n\)维超立方体组成;根据归纳假设,每个这样的超立方体都可以用\(n\)种颜色着色。 我们可以用一种不同的颜色连接两个\(n\)维超立方体的边;这将是我们的\(n + 1\)种颜色。由于这些新边总是在不同的顶点对之间,每个子立方体一个顶点,所以这些新边中没有一条会共享一个顶点,从而用\((n + 1)\)种颜色给出了\((n + 1)\)维超立方体的有效着色。
- 考虑具有偶数个 0 位的顶点和具有奇数个 0 位的顶点。每个具有偶数个 0
位的顶点仅与具有奇数个 0
位的顶点相邻,因为每条边表示一个单个位的变化(要么通过翻转 1 位添加一个
0 位,要么通过翻转 0 位删除一个 0 位)。令\(L\)为具有偶数个 0 位的顶点的集合,令\(R\)为具有奇数个 0
位的顶点的集合,那么没有两个相邻的顶点会属于同一集合。
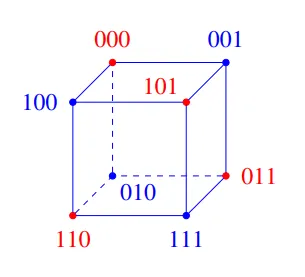
一个三维情况的示例如下(\(L\)是蓝色顶点,\(R\)是红色顶点):
- 考虑具有偶数个 0 位的顶点和具有奇数个 0 位的顶点。每个具有偶数个 0
位的顶点仅与具有奇数个 0
位的顶点相邻,因为每条边表示一个单个位的变化(要么通过翻转 1 位添加一个
0 位,要么通过翻转 0 位删除一个 0 位)。令\(L\)为具有偶数个 0 位的顶点的集合,令\(R\)为具有奇数个 0
位的顶点的集合,那么没有两个相邻的顶点会属于同一集合。
一个三维情况的示例如下(\(L\)是蓝色顶点,\(R\)是红色顶点):
替代解决方案(使用归纳法和着色):
可能更容易看出一个图是 2 可着色的等同于它是二分图。现在,论证更容易陈述。首先基础情形是一个有两个顶点的超立方体,显然是 2 可着色的。然后注意,在 2 着色中切换颜色仍然是有效的,因为如果端点颜色不同,切换会使它们仍然不同。现在,递归地对两个子立方体进行相同的 2 着色,然后在一个子立方体中切换颜色。子立方体内部的边根据归纳法是好的。跨子立方体的边也是好的,因为由于切换,相应的顶点颜色不同。
5. 模运算基础
对于前两个部分,选择与给定陈述等价的所有选项:
- \(a\equiv b(\bmod m)\)
- \(i. a\)和\(b\)除以\(m\)时具有相同的余数
- \(ii. m\mid a + b\)
- \(iii. a = b - km\),对于某个整数\(k\)
- \(a^k\equiv b^k(\bmod m)\)
- \(i. (a\bmod m)^k\equiv(b\bmod m)^k(\bmod m)\)
- \(ii. a^{k\bmod m}\equiv b^{k\bmod m}(\bmod m)\) 对于其余部分,计算每个给定数字的最后一位(或几位)数字:
- \(11^{3142}\)
- \(9^{9999}\)
- \(3^{641}\)
解决方案:
- \(i\)、\(iii\)是答案。注意对于\(ii\),\(m\mid a + b\)等价于\(a\equiv -b(\bmod m)\)。
- \(i\)是唯一答案。对于\(ii\),记住不能对指数应用取模运算。简单的反例:\(6^5\equiv4^5(\bmod4)\nRightarrow6\equiv4(\bmod4)\)。
- 首先,我们注意到\(11\equiv1(\bmod10)\)。所以\(11^{3142}\equiv1^{3142}\equiv1(\bmod10)\),所以最后一位数字是\(1\)。
- \(9\)在模\(10\)下是它自己的乘法逆元,所以\(9^2\equiv1(\bmod10)\)。然后\(9^{9999}=9^{2\times4999}\cdot9\equiv1^{4999}\cdot9\equiv9(\bmod10)\),所以最后一位数字是\(9\)。 另一种解决方案:我们知道\(9\equiv -1(\bmod10)\),所以\(9^{9999}\equiv(-1)^{9999}\equiv -1\equiv9(\bmod10)\)。你也可以用这个来表示\(9^{9999}\equiv(-1)^{9998}\cdot9\equiv9(\bmod10)\)。
- 注意到\(3^4 = 9^2\),所以利用\(9^2 = 81\equiv1(\bmod10)\),我们有\(3^4\equiv1(\bmod10)\)。我们还有\(641 = 160\times4 + 1\),所以\(3^{641}\equiv3^{4\times160}\cdot3\equiv1^{160}\cdot3\equiv3(\bmod10)\),使得最后一位数字是\(3\)。
6. 模运算杂项
证明或反驳以下陈述:
- 存在某个\(x\in\mathbb{Z}\),使得\(x\equiv3(\bmod16)\)且\(x\equiv4(\bmod6)\)。
- \(2x\equiv4(\bmod12)\Leftrightarrow x\equiv2(\bmod12)\)。
- \(2x\equiv4(\bmod12)\Leftrightarrow x\equiv2(\bmod6)\)。
解决方案:
- 不可能。 假设存在一个\(x\)满足这两个方程。由\(x\equiv3(\bmod16)\),我们有\(x = 3 + 16k\),对于某个整数\(k\)。这意味着\(x\equiv1(\bmod2)\)。由\(x\equiv4(\bmod6)\),我们有\(x = 4 + 6l\),对于某个整数\(l\)。这意味着\(x\equiv0(\bmod2)\)。现在我们有\(x\equiv1(\bmod2)\)和\(x\equiv0(\bmod2)\),矛盾。
- 假,考虑\(x\equiv8(\bmod12)\)。我们不能在第一个方程中消除\(2\)得到第二个方程的原因是\(2\)在模\(12\)下没有乘法逆元,因为\(2\)和\(12\)不互质。
- 真。我们可以将\(2x\equiv4(\bmod12)\)写成\(2x = 4 + 12k\),对于某个\(k\in\mathbb{Z}\)。除以\(2\),我们有\(x = 2 + 6k\),对于相同的\(k\in\mathbb{Z}\)。这等价于说\(x\equiv2(\bmod6)\)。
7. 模逆元
回忆讲座中逆元的定义:设\(a,m\in\mathbb{Z}\)且\(m>0\);如果\(x\in\mathbb{Z}\)满足\(ax\equiv1(\bmod m)\),那么我们说\(x\)是\(a\)模\(m\)的逆元。 现在,我们将研究逆元的存在性和唯一性。
- \(3\)是\(5\)模\(10\)的逆元吗?
- \(3\)是\(5\)模\(14\)的逆元吗?
- 对于所有\(n\in\mathbb{N}\),\(3 + 14n\)是\(5\)模\(14\)的逆元吗?
- \(4\)在模\(8\)下有逆元吗?
- 假设\(x,x'\in\mathbb{Z}\)都是\(a\)模\(m\)的逆元。有可能\(x\not\equiv x'(\bmod m)\)吗?
解决方案:
- 否,因为\(3\times5 = 15\equiv5(\bmod10)\)。
- 是,因为\(3\times5 = 15\equiv1(\bmod14)\)。
- 是,因为\((3 + 14n)\times5 = 15 + 14\times5n\equiv15\equiv1(\bmod14)\)。
- 否。为了矛盾,假设\(x\in\mathbb{Z}\)是\(4\)模\(8\)的逆元。那么\(4x\equiv1(\bmod8)\)。那么\(8\mid4x - 1\),这是不可能的。
- 否。我们有\(xa\equiv x'a\equiv1(\bmod m)\)。所以\(xa - x'a = a(x - x')\equiv0(\bmod m)\)。两边乘以\(x\),我们得到\(\begin{gathered}xa(x - x')\equiv0\cdot x(\bmod m)\\\Rightarrow x - x'\equiv0(\bmod m)\\\Rightarrow x\equiv x'(\bmod m)\end{gathered}\)
8. 斐波那契数列与最大公约数
斐波那契数列由\(F_n = F_{n - 1} + F_{n - 2}\)给出,其中\(F_0 = 0\)且\(F_1 = 1\)。证明对于所有\(n\geq1\),\(\gcd(F_n,F_{n - 1}) = 1\)。
解决方案:
通过归纳法进行。
基础情形:我们有\(\gcd(F_1,F_0)=\gcd(1,0)=1\),这是真的。
归纳假设:假设对于某个\(k\geq1\),我们有\(\gcd(F_k,F_{k - 1}) = 1\)。
归纳步骤:现在我们需要证明\(\gcd(F_{k + 1},F_k)=1\)。
我们可以证明: \(\gcd(F_{k + 1},F_k)=\gcd(F_k + F_{k - 1},F_k)=\gcd(F_k,F_{k - 1})=1\)。 注意第二个表达式来自斐波那契数列的定义。最后一个表达式来自欧几里得最大公约数算法,其中\(\gcd(x,y)=\gcd(y,x\bmod y)\),因为\(F_k + F_{k - 1}\equiv F_{k - 1}(\bmod F_k)\)。 因此,该陈述对于\(n = k + 1\)也为真。 根据归纳规则,我们可以得出对于所有\(n\geq1\),\(\gcd(F_n,F_{n - 1}) = 1\),其中\(F_0 = 0\),\(F_1 = 1\)且\(F_n = F_{n - 1} + F_{n - 2}\)。