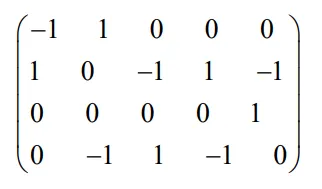SCUT2008

一、填空题

1. 求合式公式\(\forall xP(x)\to\exists xQ(x,y)\)的前束范式：

   答案：\(\forall x\exists z (P(x)\to Q(z,y))\)。

   前束范式（Prenex Normal Form）是数理逻辑中谓词逻辑公式的一种标准形式。以下是关于前束范式的详细介绍：

   定义

   一个谓词逻辑公式称为前束范式，如果它具有以下形式：\((Q_1x_1)(Q_2x_2)\cdots(Q_kx_k)B\)，其中\(Q_i\)（\(i = 1,2,\cdots,k\)）是量词（\(\forall\)或\(\exists\)），\(x_i\)是个体变元，\(B\)是不含量词的谓词公式（称为母式或基式）。

   特点

   1. 量词前置：所有的量词都被集中在公式的开头，按照一定的顺序排列，后面跟着一个不含任何量词的公式。
   2. 清晰的量词辖域结构：每个量词的辖域（即量词作用的范围）在形式上一目了然，有助于对公式进行逻辑分析和推理。

   示例

   1. 公式\(\forall x\exists y(P(x,y)\to Q(x,y))\)是前束范式，其中\(\forall x\)和\(\exists y\)是量词，\(P(x,y)\to Q(x,y)\)是母式。
   2. 而公式\(\forall x(P(x)\land\exists yQ(y))\)虽然量词都在前面，但它不是前束范式，因为\(\land\)连接了两个包含量词的部分，不满足母式不含量词的要求。通过等价变换可以化为前束范式，如\(\forall x\exists y(P(x)\land Q(y))\)。

   转换为前束范式的方法

   1. 消除量词前的否定符号：利用量词否定等价式，如\(\neg\forall xP(x)\Leftrightarrow\exists x\neg P(x)\)，\(\neg\exists xP(x)\Leftrightarrow\forall x\neg P(x)\)，将否定符号移到量词后面。
   2. 约束变元换名：如果存在不同量词约束的变元同名，为了避免混淆，使用换名规则，将其中一个变元换为其他未使用过的变元。例如，\(\forall x(P(x)\land\exists xQ(x))\)可换名为\(\forall x(P(x)\land\exists yQ(y))\)。
   3. 将量词移到公式前面：利用量词辖域扩张与收缩等价式，如\(\forall x(P(x)\land Q)\Leftrightarrow(\forall xP(x)\land Q)\)（\(x\)不在\(Q\)中自由出现），\(\exists x(P(x)\lor Q)\Leftrightarrow(\exists xP(x)\lor Q)\)（\(x\)不在\(Q\)中自由出现）等，将量词逐步移到公式的最前面。

2. 设集合\(A = \{a, b, \{a,b\}, \varnothing\}\)，\(B = \{\{a,b\}, \varnothing\}\)，求\(B - A = ?\)

   答案：\(\varnothing\)。因为\(A\)包含\(B\)中的全部元素，所以\(B-A= \varnothing\)

3. 设\(p\)与\(q\)的真值为\(0\)，\(r\)的真值为\(1\)，则命题\((p\land q)\to r\)的真值是：。

   答案：1。只有当\((p \and q)\)为真，且\(r\)为假时，\((p \and q) \rarr r\)为假，其余为真。

4. 设\(R\)是在正整数集合\(\mathbb{Z}^+\)上如下定义的二元关系：

   \[ R = \{(x,y)\mid (x,y \in \Z^+) \and x + y = 10\} \]

   则它一共有\(?\)个有序对，且有自反性、对称性、传递性、反自反性和反对称性各性质中的 ? 性质。

   答案：共有 9 个有序对，\((1,9)(2,8),(3,7)······(9,1)\)，可以发现存在\((1,9)(9,1)\)这样的有序对，所以满足对称性。

5. 公式\(\forall x(P(x)\to Q(x,y))\to S(x)\)中的自由变元为\(?\)，约束变元为\(?\)。

   答案：自由变元为\(Q(x,y)\)中的\(y\)与\(S(x)\)中的\(x\)，约束变元为\(Q(x,y)\)中的\(x\)与\(P(x)\)中的\(x\)

   1. 自由变元与约束变元的定义

   • 约束变元是在量词的辖域内出现的变元，并且该变元被量词所约束。
   • 自由变元是在公式中出现但不受任何量词约束的变元。

   2. 分析公式\(\forall x(P(x)\to Q(x,y))\to S(x)\)中的变元

   • 对于\(\forall x(P(x)\to Q(x,y))\)这部分：
   • \(x\)在量词\(\forall\)的辖域内，并且受到\(\forall\)的约束，所以\(x\)在这里是约束变元。同时\(x\)在\(P(x)\)和\(Q(x,y)\)中出现，都受到前面\(\forall x\)的约束。
   • \(y\)在\(Q(x,y)\)中出现，但是没有任何量词对\(y\)进行约束，所以\(y\)是自由变元。
   • 对于\(S(x)\)这部分：\(x\)在这里没有被任何量词约束（前面的\(\forall x\)的辖域到\(Q(x,y)\)结束），所以\(x\)是自由变元。 综上，公式\(\forall x(P(x)\to Q(x,y))\to S(x)\)中的自由变元为\(Q(x,y)\)中的\(y\)与\(S(x)\)中的\(x\)；约束变元为\(Q(x,y)\)中的\(x\)与\(P(x)\)中的\(x\)。

6. 设有命题\(T(x): x\)是火车，\(C(x): x\)是汽车，\(Q(x, y): x\)跑得比\(y\)快，那么命题“有的汽车比一些火车跑得快”的逻辑表达式是？

   答案：\(\exists x (C(x) \land \exists y(T(y) \land Q(x, y)))\)。

   1. 首先分析命题“有的汽车比一些火车跑得快”的含义：

   • “有的汽车”表示存在一个\(x\)，使得\(x\)是汽车，这可以用\(\exists x C(x)\)来表示。
   • “比一些火车跑得快”，这里需要引入另一个变量\(y\)表示火车，即存在一个\(y\)，\(y\)是火车，并且\(x\)跑得比\(y\)快，这可以表示为\(\exists y(T(y)\land Q(x,y))\)。

   2. 然后将两部分结合起来：

   • 因为要同时满足\(x\)是汽车并且存在火车\(y\)使得\(x\)比\(y\)快，所以用逻辑连接词\(\land\)将\(\exists x C(x)\)和\(\exists y(T(y)\land Q(x,y))\)连接起来，得到\(\exists x (C(x)\land\exists y(T(y)\land Q(x,y)))\)。 具体书写步骤如下：
   • 步骤一：表示存在汽车，即\(\exists x C(x)\)。
   • 步骤二：对于存在的汽车\(x\)，表示存在火车\(y\)使得\(x\)比\(y\)快，即\(\exists y(T(y)\land Q(x,y))\)。
   • 步骤三：将上述两步用\(\land\)连接起来，得到最终表达式\(\exists x (C(x)\land\exists y(T(y)\land Q(x,y)))\)。

7. 设\(G\)是\(n\)阶\(m\)条边的无向图，若\(G\)连通且\(m = ?\)，则\(G\)是无向树。

   答案：\(n-1\)。

   这里的\(n\)阶指的是\(n\)个顶点，所以是\(n\)个顶点\(m\)条边，根据树的性质，可以得到\(m=n-1\)。

8. 设\(X = \{1,2,3\}\)，\(f:X\to X\)，\(g:X\to X\)，\(f = \{\langle1, 2\rangle,\langle2,3\rangle,\langle3,1\rangle\}\)，\(g = \{\langle1,2\rangle,\langle2,3\rangle,\langle3,3\rangle\}\)，则\(f^{-1}\circ g = ?\)，\(g\circ f = ?\)

   答案：\(\{\langle1,3\rangle,\langle2,3\rangle,\langle3,2\rangle\}\)，\(\{\langle1,3\rangle,\langle2,1\rangle,\langle3,1\rangle\}\)。

   1. 首先求\(f^{-1}\)：

   • 已知\(f=\{\langle1, 2\rangle,\langle2,3\rangle,\langle3,1\rangle\}\)，那么\(f^{-1}=\{\langle2,1\rangle,\langle3,2\rangle,\langle1,3\rangle\}\)。

   2. 然后求\(f^{-1}\circ g\)：

   • 对于\(f^{-1}\circ g\)，先计算\(g(1)=2\)，再计算\(f^{-1}(2)=1\)，所以\((f^{-1}\circ g)(1)=1\)；
   • 计算\(g(2)=3\)，再计算\(f^{-1}(3)=2\)，所以\((f^{-1}\circ g)(2)=2\)；
   • 计算\(g(3)=3\)，再计算\(f^{-1}(3)=2\)，所以\((f^{-1}\circ g)(3)=2\)。
   • 综上，\(f^{-1}\circ g=\{\langle1,1\rangle,\langle2,2\rangle,\langle3,2\rangle\}\)。

   3. 接着求\(g\circ f\)：

   • 对于\(g\circ f\)，先计算\(f(1)=2\)，再计算\(g(2)=3\)，所以\((g\circ f)(1)=3\)；
   • 计算\(f(2)=3\)，再计算\(g(3)=3\)，所以\((g\circ f)(2)=3\)；
   • 计算\(f(3)=1\)，再计算\(g(1)=2\)，所以\((g\circ f)(3)=2\)。 综上，\(g\circ f=\{\langle1,3\rangle,\langle2,3\rangle,\langle3,2\rangle\}\)。 所以\(f^{-1}\circ g=\{\langle1,1\rangle,\langle2,2\rangle,\langle3,2\rangle\}\)，\(g\circ f=\{\langle1,3\rangle,\langle2,3\rangle,\langle3,2\rangle\}\)。

9. 不能再分解的命题称为原子命题，至少包含一个联结词的命题称为复合命题。

10. 连通无向图\(G\)含有欧拉回路的充分必要条件是图\(G\)中所有顶点的度数均为偶数。

11. 设集合\(A = \{\varnothing,\{a\}\}\)，则\(A\)的幂集为，\(\vert P(A)\vert = ?\)。

    答案：\(P(A) = \{\varnothing,\{\varnothing\},\{\{a\}\},\{\varnothing,\{a\}\}\}\)，4。

    幂集的大小为\(2^n\)，其中\(n\)为元素个数。

12. 设\(G = \langle V, E\rangle\)，\(G' = \langle V', E'\rangle\)为两个图(同为无向图或有向图)，若\(E'\subseteq E\)且\(V'\subseteq V\)，则称\(G'\)是\(G\)的子图，若\(E'\subseteq E\)且\(V' = V\)，则称\(G'\)是\(G\)的生成子图。

二、单选题 (本大题共 12 小题，每小题 2 分，共 26 分)

1. 下列命题公式为重言式的是（B） A. \((p\lor\neg p)\to q\) B. \(p\to (p\lor q)\) C. \(q\land\neg q\) D. \((p\to p)\to q\)

   答案：B。重言式，即永真式。

   1. 对于选项 A：

   • 公式\((p\lor\neg p)\to q\)，其中\(p\lor\neg p\)恒为真（排中律），但是当\(q\)为假时，整个式子为假，所以它不是重言式。

   2. 对于选项 B：

   • 公式\(p\to(p\lor q)\)，当\(p\)为真时，\(p\lor q\)一定为真，根据蕴含式的定义，前件真后件真，整个式子为真；当\(p\)为假时，根据蕴含式的定义，前件假整个式子为真。所以无论\(p\)和\(q\)取何值，该公式都为真，它是重言式。

   3. 对于选项 C：

   • 公式\(q\land\neg q\)恒为假（矛盾律），所以它不是重言式。

   4. 对于选项 D：

   • 公式\((p\to p)\to q\)，\(p\to p\)恒为真，但是当\(q\)为假时，整个式子为假，所以它不是重言式。

2. 下列语句中为命题的是（D） A. 你好吗？ B. 人有\(6\)指。 C. 我所说的是假的。 D. 明天是晴天。 答案：D。

   1. 首先分析命题的定义：

   • 命题是能够判断真假的陈述句。

   2. 然后看选项 A：

   • “你好吗？”这是一个疑问句，不是陈述句，所以它不是命题。

   3. 再看选项 B：

   • “人有\(6\)指”，这句话虽然是陈述句，但是它的真假取决于具体情况，在没有明确的语境或定义下，无法确定其真假，所以它不是命题。

   4. 接着看选项 C：

   • “我所说的是假的”，这句话会产生自指的矛盾情况，无法确定其真假，所以它不是命题。

   5. 最后看选项 D：

   • “明天是晴天”是一个陈述句，并且在给定的时间（明天）到来后，可以判断其真假，所以它是命题。

3. 设\(D = \langle V, E\rangle\)为有向图，\(V = \{a, b, c, d, e, f\}\)，\(E = \{\langle a, b\rangle, \langle b, c\rangle, \langle a, d\rangle, \langle d, e\rangle, \langle f, e\rangle\}\)是（C） A. 强连通图 B. 单向连通图 C. 弱连通图 D. 不连通图

   答案：注意是有向图，选择 C。

   1. 首先明确各种连通图的定义：

   • 强连通图：在有向图中，如果对于每一对顶点\(u\)和\(v\)，都存在从\(u\)到\(v\)和从\(v\)到\(u\)的路径，则称该有向图是强连通图。
   • 单向连通图：如果对于有向图中的任意两个顶点\(u\)和\(v\)，至少存在从\(u\)到\(v\)或者从\(v\)到\(u\)的路径，则称该有向图是单向连通图。
   • 弱连通图：将有向图的所有有向边替换为无向边后得到的无向图是连通的，则称该有向图是弱连通图。
   • 不连通图：如果图中存在顶点对，它们之间没有路径相连（无论是有向路径还是无向路径，在有向图中考虑无向路径时是将边视为无向的情况），则称该图是不连通图。

   2. 然后分析给定的有向图\(D\)：

   • 把有向图\(D\)的有向边替换为无向边后，得到的无向图是连通的（可以通过简单观察或者尝试从任意一个顶点出发能否到达其他顶点来判断，例如从\(a\)可以通过\(b\)、\(c\)到达\(e\)，从\(a\)也可以通过\(d\)到达\(e\)等）。
   • 但是，在有向图\(D\)中，例如从\(e\)到\(a\)就不存在路径，不满足强连通图的定义；同时也不满足单向连通图的定义（存在一些顶点对，既没有从一个到另一个的有向路径，也没有反向的有向路径）。

4. 集合\(A = \{a, b, c\}\)上的下列关系矩阵中符合偏序关系条件的是（） A. \(\begin{pmatrix}1&0&1&0\\0&1&1&0\\0&0&1&1\\1&1&0&1\end{pmatrix}\) B. \(\begin{pmatrix}1&0&1\\0&1&0\\1&0&1\end{pmatrix}\) C. \(\begin{pmatrix}1&0&1\\1&1&0\\0&0&1\end{pmatrix}\) D. \(\begin{pmatrix}1&1&1\\0&1&0\\0&1&1\end{pmatrix}\)

   答案：D。

   偏序关系的定义及性质

   1. 自反性：对于集合\(A\)中的任意元素\(a\)，都有\((a,a)\in R\)。在关系矩阵中体现为主对角线元素全为\(1\)。
   2. 反对称性：如果\((a,b)\in R\)且\((b,a)\in R\)，那么\(a = b\)。在关系矩阵中，如果\(i\neq j\)且\(a_{ij}=1\)，则\(a_{ji}=0\)。
   3. 传递性：若\((a,b)\in R\)且\((b,c)\in R\)，则\((a,c)\in R\)。从关系矩阵角度看，如果\(a_{ij}=1\)且\(a_{jk}=1\)，那么\(a_{ik}=1\)。

   对选项 A 的分析

   关系矩阵\(\begin{pmatrix}1&0&1&0\\0&1&1&0\\0&0&1&1\\1&1&0&1\end{pmatrix}\)：

   • 主对角线元素全为\(1\)，满足自反性。
   • 满足反对称性。
   • 传递性不满足，缺少\(1,2\)的关系

   对选项 B 的分析

   关系矩阵\(\begin{pmatrix}1&0&1\\0&1&0\\1&0&1\end{pmatrix}\)：

   • 主对角线元素全为\(1\)，满足自反性。
   • 当\(i = 1\)，\(j = 3\)时\(a_{13}=1\)，当\(i = 3\)，\(j = 1\)时\(a_{31}=1\)，且\(1\neq3\)，不满足反对称性，所以选项 B 不符合偏序关系条件。

   对选项 C 的分析

   关系矩阵\(\begin{pmatrix}1&0&1\\1&1&0\\0&0&1\end{pmatrix}\)：

   • 主对角线元素全为\(1\)，满足自反性。
   • 满足反对称性。
   • 缺少传递性。

   对选项 D 的分析

   关系矩阵\(\begin{pmatrix}1&1&1\\0&1&0\\0&1&1\end{pmatrix}\)：

   • 主对角线元素全为\(1\)，满足自反性。
   • 对于反对称性，不存在\(i\neq j\)使得\(a_{ij}=1\)且\(a_{ji}=1\)的情况，满足反对称性。
   • 对于传递性，例如\(a_{12}=1\)且\(a_{23}=0\)，此时不需要考虑\(a_{13}\)是否为\(1\)（因为传递性的前提是两个关系都存在）；再看\(a_{13}=1\)，可以看作是因为\(a_{11}=1\)且\(a_{13}=1\)（从\(a\)到\(a\)再到\(c\)的一种特殊传递情况，因为\(a\)到自身的关系总是存在的）；其他情况也都满足传递性。所以选项 D 符合偏序关系条件。

5. 设\(A = \{1, 2, 3\}\)，\(A\)上二元关系\(S = \{\langle1, 1\rangle, \langle1, 2\rangle, \langle3, 2\rangle, \langle3, 3\rangle\}\)，则\(S\)是（B） A. 自反关系 B. 传递关系 C. 对称关系 D. 反自反关系 答案：B

   1. 首先明确各种关系的定义：

   • 自反关系：对于集合\(A\)中的每一个元素\(a\)，都有\((a,a)\in R\)。
   • 传递关系：如果\((a,b)\in R\)且\((b,c)\in R\)，那么\((a,c)\in R\)。
   • 对称关系：如果\((a,b)\in R\)，那么\((b,a)\in R\)。
   • 反自反关系：对于集合\(A\)中的每一个元素\(a\)，都有\((a,a)\notin R\)。

   2. 然后分析关系\(S\)：

   • 对于自反关系，集合\(A=\{1,2,3\}\)，但是\((2,2)\notin S\)，所以\(S\)不是自反关系。
   • 对于传递关系，有\((1,2)\in S\)和\((3,2)\in S\)，不存在\((1,3)\)这种情况，不会出现违背传递性的情况，其他元素对之间也满足传递性定义（例如\((1,1)\in S\)且\((1,2)\in S\)，\((1,2)\in S\)满足传递；\((3,2)\in S\)且\((3,3)\in S\)，不存在\((2,3)\in S\)所以也满足传递等），所以\(S\)是传递关系。
   • 对于对称关系，\((1,2)\in S\)，但是\((2,1)\notin S\)，所以\(S\)不是对称关系。
   • 对于反自反关系，因为\((1,1)\in S\)和\((3,3)\in S\)，所以\(S\)不是反自反关系。

6. 设\(A = \{a,b,c,d\}\)，\(A\)上的等价关系\(R = \{\langle a, b\rangle, \langle b, a\rangle, \langle c, d\rangle, \langle d, c\rangle\}\cup I_A\)，则对应于\(R\)的\(A\)的划分是（D） A. \(\{\{a\},\{b, c\},\{d\}\}\) B. \(\{\{a, b\},\{c\}, \{d\}\}\) C. \(\{\{a\},\{b\},\{c\},\{d\}\}\) D. \(\{\{a, b\}, \{c,d\}\}\)

   答案：D。注意等价关系的三个前提：自反性，对称性，传递性

   1. 首先明确等价关系与划分的关系：

   • 等价关系会将集合划分为互不相交的子集（等价类），使得同一子集中的元素相互等价（在关系\(R\)下）。

   2. 然后分析等价关系\(R\)：

   • 对于\(\langle a,b\rangle,\langle b,a\rangle\in R\)以及\(I_A\)中包含\(\langle a,a\rangle,\langle b,b\rangle\)，这说明\(a\)和\(b\)是等价的，它们属于同一个等价类，即\(\{a,b\}\)。
   • 对于\(\langle c,d\rangle,\langle d,c\rangle\in R\)以及\(I_A\)中包含\(\langle c,c\rangle,\langle d,d\rangle\)，这说明\(c\)和\(d\)是等价的，它们属于同一个等价类，即\(\{c,d\}\)。

   3. 最后看选项：

   • 选项 A 中\(\{b,c\}\)不符合\(a\)与\(b\)等价、\(c\)与\(d\)等价的情况。
   • 选项 B 中\(\{c\}\)和\(\{d\}\)没有将\(c\)和\(d\)放在同一个等价类中。
   • 选项 C 中没有体现出\(a\)与\(b\)等价、\(c\)与\(d\)等价形成的等价类。
   • 选项 D 中\(\{\{a,b\},\{c,d\}\}\)正确地反映了由等价关系\(R\)确定的\(A\)的划分。

7. 以下非负整数列可简单图化为一个欧拉图的是（D） A. \(\{2, 2, 2, 2, 0\}\) B. \(\{4, 2, 6, 2, 2\}\) C. \(\{2, 2, 3, 4, 1\}\) D. \(\{4, 2, 2, 4, 2\}\)

   答案：D。

   1. 首先明确欧拉图的判定条件：

   • 一个无向图是欧拉图当且仅当该图是连通的且所有顶点的度数均为偶数。

   2. 然后分析每个选项所代表的图的度数序列：

   • 选项 A：\(\{2, 2, 2, 2, 0\}\)，有一个顶点度数为\(0\)，这意味着该图不连通（孤立顶点），所以不能是欧拉图。
   • 选项 B：\(\{4, 2, 6, 2, 2\}\)，所有顶点度数之和为\(4 + 2+6 + 2+2 = 16\)，根据握手定理（在无向图中，所有顶点的度数之和等于边数的两倍），边数为\(16\div2 = 8\)。但是如果尝试构建这样一个图，会发现无法满足所有顶点度数的要求（例如，一个顶点度数为\(6\)，很难在只有\(8\)条边且其他顶点度数较小的情况下构建出符合条件的图），所以该序列不能简单图化为欧拉图。
   • 选项 C：\(\{2, 2, 3, 4, 1\}\)，其中有顶点度数为\(3\)和\(1\)，不满足所有顶点度数均为偶数的条件，所以不能是欧拉图。
   • 选项 D：\(\{4, 2, 2, 4, 2\}\)，所有顶点度数均为偶数，并且可以尝试构建出一个连通的图满足这些度数要求（例如，一个五边形，其中两个不相邻顶点之间再加两条边，就可以使五个顶点的度数分别为\(4,2,2,4,2\)），所以该序列可以简单图化为欧拉图。

8. 设论域\(D = \{a, b\}\)，与公式\(\forall xA(x)\)等价的命题公式是（C） A. \(A(a)\land A(b)\) B. \(A(a)\to A(b)\) C. \(A(a)\lor A(b)\) D. \(A(b)\to A(a)\)

   答案：C。

9. 一棵树有\(3\)个\(4\)度顶点，\(4\)个\(2\)度顶点，其余都是树叶，求这棵树有多少个树叶顶点（B） A. \(12\) B. \(8\) C. \(10\) D. \(13\)

   答案：B。使用握手定理解决即可。

   1. 首先设树叶顶点的个数为\(x\)。
   2. 然后根据树的性质，树的边数\(m=n - 1\)（其中\(n\)是顶点数），以及握手定理（所有顶点的度数之和等于边数的两倍）来计算。

   • 已知有\(3\)个\(4\)度顶点，其度数和为\(3\times4 = 12\)；有\(4\)个\(2\)度顶点，其度数和为\(4\times2 = 8\)；树叶顶点度数为\(1\)，\(x\)个树叶顶点度数和为\(x\)。
   • 那么所有顶点的度数之和为\(12 + 8+x\)。
   • 顶点数\(n=3 + 4+x=7 + x\)，边数\(m = n - 1 = 6 + x\)。
   • 根据握手定理可得\(12 + 8+x = 2(6 + x)\)。

   3. 接着解方程：

   • \(12 + 8+x = 12 + 2x\)
   • 移项可得\(2x - x = 12 + 8 - 12\)
   • 解得\(x = 8\)。

10. 有\(A\)、\(B\)、\(C\)三个人猜测甲乙丙三个球队中的冠军。各人的猜测如下： A: 冠军不是甲，也不是乙。 B: 冠军不是甲，而是丙。 C: 冠军不是丙，而是甲。 已知其中有一个人说的完全正确，一个人说的都不对，而另外一人恰有一半说对了。据此推算，冠军应该是（A） A. 甲 B. 乙 C. 丙 D. 不确定

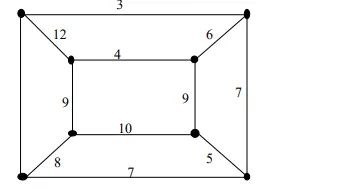
11. 如第 11 题图所示各图，其中存在哈密顿回路的图是（C）

    答案：C

    • A，存在一个孤立点没有被访问，所以不行。

    • B，中间点必须访问两次，不行。

    • C，可以直接沿着正方形四条边进行访问。

    • D，必须经过中间点，所以不行。

    这是一道关于判断图中哪些图存在哈密顿回路的题目，答案是 (C)。

    解析

    1. 哈密顿回路的定义

    • 哈密顿回路是指在一个图中，从一个顶点出发，经过图中每个顶点恰好一次，最后回到起始顶点的路径。

    2. 对各选项的分析

    • 选项 (A)
    • 这是一个三角形加上一个孤立点。由于存在孤立点，无法形成经过所有顶点的回路，所以不存在哈密顿回路。
    • 选项 (B)
    • 这是一个带有交叉线的四边形。无论从哪个顶点出发，在经过所有顶点且仅经过一次的情况下，都无法回到起始顶点形成回路。例如，从左上角顶点出发，经过其他三个顶点后，无法再回到左上角顶点形成回路，所以不存在哈密顿回路。
    • 选项 (C)
    • 这是一个完整的四边形。可以很容易地找到哈密顿回路，例如按照顺时针或逆时针方向依次经过四个顶点，最后回到起始顶点，所以存在哈密顿回路。
    • 选项 (D)
    • 这是一个类似蝴蝶结形状的图。在尝试寻找哈密顿回路时会发现，无论从哪个顶点出发，都无法在经过每个顶点恰好一次的情况下回到起始顶点。例如，从上方中间顶点出发，经过其他顶点时，总会有顶点无法在满足条件的情况下被访问到，所以不存在哈密顿回路。

12. 设\(C(x): x\)是国家级运动员，\(G(x): x\)是健壮的，则命题“没有一个国家级运动员不是健壮的”可符号化为（\(\neg\exists x(C(x)\land\neg G(x))\)）

三、计算题(30 分)

1. 用等值演算法求取求下列公式：\(((\urcorner P\rarr Q)\rarr( P\or \urcorner Q))\)的合取范式。

\[ \Leftrightarrow (P\or Q) \rarr (P \or \urcorner Q)\\ \Leftrightarrow \urcorner(P \or Q) \or (P \or \urcorner Q) \\ \Leftrightarrow (\urcorner P \and \urcorner Q)\or (P \or \urcorner Q) \\ \Leftrightarrow ((\urcorner P \and \urcorner Q) \or P)\or \urcorner Q \\ \Leftrightarrow ((\urcorner P \or P)\and(\urcorner Q\or P)) \or \urcorner Q \\ \Leftrightarrow (\urcorner Q \or P) \or \urcorner Q \\ \Leftrightarrow P \or \urcorner Q \]

2. 图\(G\)如下图所示，求图\(G\)的最小生成树。（图略，可根据边的权重选择合适的边构建最小生成树，此处省略具体过程）

   

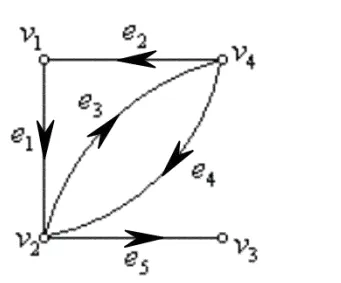
3. 有向图\(D\)如图所示，求\(D\)的关联矩阵\(M(D)\)。（图略，根据有向图关联矩阵的定义写出矩阵，此处省略具体矩阵内容）

   

   答案：-1 表示起点，1 是终点。

   横坐标表示的是\(edge\)，纵坐标表示的是\(vertix\)

   

4. 化简表达式

   \[ (((A \cup(B-C))\cap A) \cup(B-(B-A)))\cap(C-A) \]

   答案：

   \(B-A=B-AB=B\overline{A}\)，故\(B-(B-A)=B-B\overline{A}=BA\)

   1. 首先化简\(B-(B - A)\)：

   • 根据集合差的定义，\(B-(B - A)=B\cap(\overline{B - A})\)。
   • 又因为\(B - A = B\cap\overline{A}\)，所以\(\overline{B - A}=\overline{B\cap\overline{A}}=\overline{B}\cup A\)。
   • 则\(B-(B - A)=B\cap(\overline{B}\cup A)=(B\cap\overline{B})\cup(B\cap A)=B\cap A\)。

   2. 然后化简\((A\cup(B - C))\cap A\)：

   • 根据分配律\((A\cup(B - C))\cap A=(A\cap A)\cup((B - C)\cap A)=A\cup((B - C)\cap A)\)。
   • 因为\((B - C)\cap A=(B\cap\overline{C})\cap A\)，所以\((A\cup(B - C))\cap A = A\cup((B\cap\overline{C})\cap A)=A\)（因为\(A\cup(A\cap X)=A\)，这里\(X=(B\cap\overline{C})\)）。

   3. 接着将化简后的结果代入原式：

   • 原式变为\((A\cup(B\cap A))\cap(C - A)\)。
   • 根据分配律\((A\cup(B\cap A))=(A\cup B)\cap(A\cup A)=(A\cup B)\cap A = A\)（因为\(A\cup B\)与\(A\)取交还是\(A\)）。
   • 所以原式变为\(A\cap(C - A)\)。
   • 又因为\(C - A=C\cap\overline{A}\)，所以\(A\cap(C - A)=A\cap(C\cap\overline{A})=(A\cap\overline{A})\cap C=\varnothing\cap C=\varnothing\)。 综上，化简结果为\(\varnothing\)。

5. 设\(R = \{\langle2, 1\rangle, \langle2, 5\rangle, \langle2, 4\rangle, \langle3, 4\rangle, \langle4, 4\rangle, \langle5, 2\rangle\}\)，求\(r(R)\)和\(s(R)\)，并作出它们及\(R\)的关系图。

   答案：

\[ r(R) = R\cup I_A = \{\langle2, 1\rangle, \langle2, 5\rangle, \langle2, 4\rangle, \langle3, 4\rangle, \langle4, 4\rangle, \langle5, 2\rangle,\langle1,1\rangle,\langle2,2\rangle,\langle3,3\rangle,\langle4,4\rangle,\langle5,5\rangle\} \\ s(R) = R\cup R^{-1} = \{\langle2, 1\rangle, \langle1, 2\rangle, \langle2, 5\rangle, \langle5, 2\rangle, \langle2, 4\rangle, \langle4, 2\rangle, \langle3, 4\rangle, \langle4, 3\rangle, \langle4, 4\rangle\} \]

1. 求\(r(R)\)（自反闭包）

• 定义：设\(R\)是集合\(A\)上的关系，\(r(R)=R\cup I_A\)，其中\(I_A = \{\langle a,a\rangle|a\in A\}\)是\(A\)上的恒等关系。
• 已知\(R = \{\langle2, 1\rangle, \langle2, 5\rangle, \langle2, 4\rangle, \langle3, 4\rangle, \langle4, 4\rangle, \langle5, 2\rangle\}\)，假设\(A=\{1,2,3,4,5\}\)（因为\(R\)中的元素涉及到这些数字）。
• 那么\(I_A=\{\langle1,1\rangle,\langle2,2\rangle,\langle3,3\rangle,\langle4,4\rangle,\langle5,5\rangle\}\)。
• 所以\(r(R)=R\cup I_A=\{\langle2, 1\rangle, \langle2, 5\rangle, \langle2, 4\rangle, \langle3, 4\rangle, \langle4, 4\rangle, \langle5, 2\rangle,\langle1,1\rangle,\langle2,2\rangle,\langle3,3\rangle,\langle4,4\rangle,\langle5,5\rangle\}\)。

2. 求\(s(R)\)（对称闭包）

• 定义：设\(R\)是集合\(A\)上的关系，\(s(R)=R\cup R^{-1}\)，其中\(R^{-1}=\{\langle b,a\rangle|\langle a,b\rangle\in R\}\)。
• 对于\(R = \{\langle2, 1\rangle, \langle2, 5\rangle, \langle2, 4\rangle, \langle3, 4\rangle, \langle4, 4\rangle, \langle5, 2\rangle\}\)，其逆关系\(R^{-1}=\{\langle1,2\rangle,\langle5,2\rangle,\langle4,2\rangle,\langle4,3\rangle,\langle4,4\rangle,\langle2,5\rangle\}\)。
• 所以\(s(R)=R\cup R^{-1}=\{\langle2, 1\rangle, \langle1, 2\rangle, \langle2, 5\rangle, \langle5, 2\rangle, \langle2, 4\rangle, \langle4, 2\rangle, \langle3, 4\rangle, \langle4, 3\rangle, \langle4, 4\rangle\}\)。

3. 关系图绘制

• 关系\(R\)的关系图：
• 用五个点分别表示\(1\)、\(2\)、\(3\)、\(4\)、\(5\)。
• 对于\(\langle2, 1\rangle\)，从点\(2\)画箭头指向点\(1\)；对于\(\langle2, 5\rangle\)，从点\(2\)画箭头指向点\(5\)；对于\(\langle2, 4\rangle\)，从点\(2\)画箭头指向点\(4\)；对于\(\langle3, 4\rangle\)，从点\(3\)画箭头指向点\(4\)；对于\(\langle4, 4\rangle\)，从点\(4\)画一个自环；对于\(\langle5, 2\rangle\)，从点\(5\)画箭头指向点\(2\)。
• 关系\(r(R)\)的关系图：
• 在\(R\)的关系图基础上，再给点\(1\)、\(2\)、\(3\)、\(4\)、\(5\)分别加上自环（因为\(r(R)\)包含恒等关系）。
• 关系\(s(R)\)的关系图：
• 在\(R\)的关系图基础上，对于\(R\)中的每一个有序对\(\langle a,b\rangle\)，如果\(R\)中没有\(\langle b,a\rangle\)，则添加从\(b\)指向\(a\)的箭头。例如，因为\(R\)中有\(\langle2, 1\rangle\)，添加从\(1\)指向\(2\)的箭头；因为\(R\)中有\(\langle2, 5\rangle\)，已有\(\langle5, 2\rangle\)，不用添加；因为\(R\)中有\(\langle2, 4\rangle\)，添加从\(4\)指向\(2\)的箭头；因为\(R\)中有\(\langle3, 4\rangle\)，添加从\(4\)指向\(3\)的箭头。

五、证明题(22 分)

1. 构造下面推理的证明：

   前提：

   \[ p \or q, p \rarr \urcorner r, s\rarr t, \urcorner s \rarr r, \urcorner t \]

   结论：\(q\)。

   答案：总结思路就是从\(t\rarr s \rarr r \rarr p \rarr q\)

   • \(\urcorner t\)前提引入
   • \(s \rarr t\)前提引入
   • \(\urcorner s\)取拒式（利用\(s \rarr t\)的逆否命题：\(\urcorner t \rarr \urcorner s\)）
   • \(\urcorner s \rarr r\)前提引入
   • \(r\)假言推理
   • \(p \rarr \urcorner r\)前提引入
   • \(\urcorner p\)取拒式
   • \(p \or q\)前提引入
   • \(q\)析取三段论

2. 设\(A = \{1, 2, 3, 4\}\)，在\(A \times A\)上定义的二元关系\(R\)，\(\forall \langle u,v \rangle,\langle x,y \rangle \in A \times A,\langle u,v \rangle R \langle x,y \rangle \Leftrightarrow u+y = x+v\).

   证明\(R\)是\(A \times A\)上的等价关系。

   答案：

   • 自反性：取\(\forall \langle u,v \rangle \in A \times A\)

     \(\Rightarrow u +v = u + v\)

     \(\Rightarrow \langle u, v \rangle R \langle u,v \rangle\)

     故自反性得证。

   • 对称性：\(\forall \langle u,v \rangle \langle x,y \rangle \in A \times A\)且\(\langle u,v \rangle R \langle x,y \rangle\)

     \(\Rightarrow u+y=x+v\)

     \(\Rightarrow x+v = u+y\)

     \(\langle x, y \rangle R \langle u,v \rangle\)

     故对称性得证。

   • 传递性：

     \(\forall \langle u, v \rangle \langle x, y \rangle \langle m,n \rangle \in A \times A\)且\(\langle u,v \rangle R\langle x,y \rangle,\langle x,y \rangle R \langle m,n \rangle\)。

     \(\Rightarrow u+y=v+x,x+n=y+m\)

     \(\Rightarrow u-v=x-y,x-y=m-n\)

     \(\Rightarrow u-v=m-n\)

     \(\Rightarrow u+n=m+v\)

     \(\Rightarrow \langle u,v \rangle R \langle m,n \rangle\)

     故满足传递性。

3. 已知：\(A,B,C\)是三个集合，证明\(A-(B \cup C)=(A-B) \cap(A-C)\)。

   答案：

   • 设\(\forall x \in (A-(B \cup C))\)
   • \(x \in (A-(B \cup C))\)
   • \(\Leftrightarrow x \in A \and x \notin (B \cup C)\)
   • \(\Leftrightarrow x \in A \and(x \notin B \and x \notin C)\)
   • \(\Leftrightarrow x \in A \and x \notin B \and x \in A \and x\notin C\)
   • \(\Leftrightarrow x \in ((A-B)\and (A-C))\)
   • 原命题得证。

4. 无向图\(G=\langle V,E \rangle\)，且\(|V|=n,|E|=m\), 试证明以下两个命题是等价命题：

   1）\(G\) 中每对顶点间具有唯一的通路

   2）\(G\) 连通且 \(n=m+1\)。

   证明：

   1. 首先证明\(1)\Rightarrow2)\)：

   • 假设\(G\)中每对顶点间具有唯一的通路。
   • 证明\(G\)连通：因为每对顶点间都有通路，所以\(G\)是连通图。
   • 证明\(n = m+1\)：
   • 对\(n\)进行归纳。
   • 当\(n = 1\)时，\(m = 0\)，此时\(n=m + 1\)成立。
   • 假设当\(n=k\)时命题成立，即对于有\(k\)个顶点的满足条件的图\(G_{k}\)，有\(m_{k}=k - 1\)。
   • 当\(n=k + 1\)时，在图\(G\)中任取一条边\(e=\{u,v\}\)，由于\(G\)中每对顶点间具有唯一的通路，去掉边\(e\)后，\(G\)变成两个连通分支\(G_{1}\)和\(G_{2}\)，设\(|V(G_{1})|=n_{1}\)，\(|V(G_{2})|=n_{2}\)，且\(n_{1}+n_{2}=k + 1\)。
   • 由归纳假设，\(|E(G_{1})|=n_{1}-1\)，\(|E(G_{2})|=n_{2}-1\)。
   • 而原来的图\(G\)的边数\(m=(n_{1}-1)+(n_{2}-1)+1=n_{1}+n_{2}-1=(k + 1)-1\)，即\(m=n - 1\)，也就是\(n=m + 1\)。

   2. 然后证明\(2)\Rightarrow1)\)：

   • 假设\(G\)连通且\(n=m + 1\)。
   • 反证法证明每对顶点间具有唯一的通路：假设存在一对顶点\(u\)和\(v\)，它们之间有两条不同的通路\(P_{1}\)和\(P_{2}\)。
   • 设\(C = P_{1}\cup P_{2}\)，\(C\)中必存在圈。
   • 设\(C\)中的圈有\(l\)个顶点，\(l\geqslant3\)，从\(G\)中去掉\(C\)中的一条边\(e\)，得到的图\(G - e\)仍然是连通的。
   • 设\(G - e\)有\(n\)个顶点和\(m-1\)条边，且\(n-(m - 1)=n-m + 1\)。
   • 因为\(n=m + 1\)，所以\(n-m + 1 = 2\)，这与树的性质\(n=m + 1\)矛盾（因为去掉边后若还连通就不是树了，树中任意两点间有唯一通路）。
   • 所以\(G\)中每对顶点间具有唯一的通路。 综上，两个命题是等价命题。