ABC062

[ABC062A] Grouping

题面翻译

题目描述

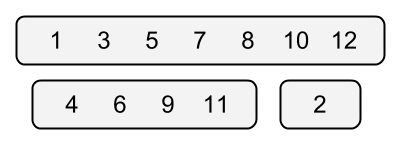
现在有两个序（如下图）

给你两个数，问你这两个数是不是在同一个序列里面的。

输入格式

一行，两个整数x,y(1≤x,y≤12)。

输出格式

一行如果x和y在同一个序列里，就输出Yes，否则输出No。

输入样例1

1 3

输出样例1

Yes

输入样例2

2 4

输出样例2

No

题目描述

すぬけ君は、$ 1 $ から $ 12 $ までの整数を下図のようにグループ分けしました。 整数 $ x $, $ y $ ($ 1 < = x < y < = 12 \() が与えられるので、\) x $, $ y $ が同一のグループに属しているか判定してください。

b4ab979900ed647703389d4349eb84ee.png

输入格式

入力は以下の形式で標準入力から与えられる。

$ x $ $ y $

输出格式

$ x $, $ y $ が同一のグループに属しているならば Yes を、そうでなければ No を出力せよ。

样例 #1

样例输入 #1

1 3

样例输出 #1

Yes

样例 #2

样例输入 #2

2 4

样例输出 #2

No

提示

制約

• $ x $, $ y $ は整数である。
• $ 1 < = x < y < = 12 $

思路

有趣的事情，这些数对应的恰好是对应月份的天数

#include<iostream>
using namespace std;
int a[12]={31,28,31,30,31,30,31,31,30,31,30,31};
int main()
{
	int b,c;
    cin>>b>>c;
	if(a[b-1]==a[c-1]) cout<<"Yes";//判断
	else cout<<"No";
    return 0;//比赛时不可少
}

[ABC062B] Picture Frame

题面翻译

题目描述

给出一个长H，宽W的图像，用小写字母表示。第i行第j个字母是a(i,j)。

输出该图像最外层用一个'#'包围后的图像

输入格式

输入将会按照以下格式：

H W
a(1,1) ... a(1,W)
...
a(H,1) ... a(H,W)

输出格式

输出该图像最外层用一个'#'包围后的图像

说明/提示

1 \(\le\) H,W \(\le\) 100

a(i,j)是一个小写字母

题目描述

縦 $ H $ ピクセル、横 $ W $ ピクセルの画像があります。 各ピクセルは英小文字で表されます。 上から $ i $ 番目、左から $ j $ 番目のピクセルは $ a_{ij} $ です。

この画像の周囲 $ 1 $ ピクセルを # で囲んだものを出力してください。

输入格式

入力は以下の形式で標準入力から与えられる。

$ H $ $ W $ $ a_{11} $ $ ... $ $ a_{1W} $ $ : $ $ a_{H1} $ $ ... $ $ a_{HW} $

输出格式

画像の周囲 $ 1 $ ピクセルを # で囲んだものを出力せよ。

样例 #1

样例输入 #1

2 3
abc
arc

样例输出 #1

#####
#abc#
#arc#
#####

样例 #2

样例输入 #2

1 1
z

样例输出 #2

###
#z#
###

提示

制約

• $ 1 < = H, W < = 100 $
• $ a_{ij} $ は英小文字である。

思路

直接模拟即可

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const double PI=acos(-1);
const int MAXN=1e5+10;
const ll mod=1e9+7;
const ll INF=1e9;
char a[110][110];
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int h,w;
    cin>>h>>w;
    for(int i=1;i<=h;i++)
        for(int j=1;j<=w;j++)
            cin>>a[i][j];
    for(int i=1;i<=w+2;i++){
        cout<<"#";
    }
    cout<<endl;
    for(int i=1;i<=h;i++){
        cout<<"#";
        for(int j=1;j<=w;j++){
            cout<<a[i][j];
        }
        cout<<"#\n";
    }
    for(int i=1;i<=w+2;i++){
        cout<<"#";
    }
    return 0;
}

[ABC062C] Chocolate Bar

题面翻译

给定一个大小为 \(H \times W\) 的矩形，由 \(H \times W\) 个小矩形组成。

你需要将这个大矩形切成三个部分，要求只能沿着小矩形的边切且且出来的三个部分必须均为矩形。

请最小化切出来的三个矩形中最大矩形与最小矩形的差，并输出这个差值。

题目描述

縦 $ H $ ブロック、横 $ W $ ブロックの板チョコがあります。 すぬけ君は、この板チョコをちょうど $ 3 $ つのピースに分割しようとしています。 ただし、各ピースはブロックの境目に沿った長方形でなければなりません。

すぬけ君は、$ 3 $ つのピースの面積 (ブロック数) をできるだけ均等にしようとしています。 具体的には、$ 3 $ つのピースの面積の最大値を $ S_{max} $、最小値を $ S_{min} $ としたとき、$ S_{max} - S_{min} $ を最小化しようとしています。 $ S_{max} - S_{min} $ の最小値を求めてください。

输入格式

入力は以下の形式で標準入力から与えられる。

$ H $ $ W $

输出格式

$ S_{max} - S_{min} $ の最小値を出力せよ。

样例 #1

样例输入 #1

3 5

样例输出 #1

0

样例 #2

样例输入 #2

4 5

样例输出 #2

2

样例 #3

样例输入 #3

5 5

样例输出 #3

4

样例 #4

样例输入 #4

100000 2

样例输出 #4

1

样例 #5

样例输入 #5

100000 100000

样例输出 #5

50000

提示

制約

• $ 2 < = H, W < = 10^5 $

Sample Explanation 1

次図のように分割すると、$ S_{max} - S_{min} = 5 - 5 = 0 $ となります。 

Sample Explanation 2

次図のように分割すると、$ S_{max} - S_{min} = 8 - 6 = 2 $ となります。 

Sample Explanation 3

次図のように分割すると、$ S_{max} - S_{min} = 10 - 6 = 4 $ となります。 

思路

其实很好想：暴力枚举。先横切一刀，再竖切一刀。

可以先枚举横切的一块，再将剩下的一块一分为二，尽可能均分。

注意有两个横切的方向，并且要比较横切块与竖切块的大小关系。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const double PI=acos(-1);
const int MAXN=1e5+10;
const ll mod=1e9+7;
const ll INF=1e9;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    ll h,w;
    cin>>h>>w;
    
    //特判，如果为三的倍数，直接为0
    if(h%3==0||w%3==0)cout<<0;
    
    //一般情况
    else{
        ll cnt=0;
        ll ans=1e15;
        
        //枚举横切，这是其中一个方向
        for(ll i=1;i<=h;i++){
            cnt+=w;
            
            //竖切能均分
            if((h*w-cnt)%2==0){
                ans=min(ans,abs((h*w-cnt)/2-cnt));
            }
            
            //竖切不能均分，需要选出最大最小
            else{
                ll MAX=max(cnt,(h*w-cnt+h-i)/2);
                ll MIN=min(cnt,(h*w-cnt-h+i)/2);
                ans=min(ans,MAX-MIN);
            }
        }
        cnt=0;
        ll ans2=1e15;
        
        //另外一个方向
        for(ll i=1;i<=w;i++){
            cnt+=h;
            
            //竖切能均分
            if((h*w-cnt)%2==0){
                ans2=min(ans2,abs((h*w-cnt)/2-cnt));
            }
            
            //竖切不能均分
            else{
                ll MAX=max(cnt,(h*w-cnt+w-i)/2);
                ll MIN=min(cnt,(h*w-cnt-w+i)/2);
                ans2=min(ans2,MAX-MIN);
            }
        }
        cout<<min(ans,ans2);
    }
    return 0;
}

[ABC062D] 3N Numbers

题面翻译

给一个长度为 \(3N\) 的数组 \(a=(a_1,a_2,...,a_n)\)，要求删去其中 \(N\) 个数使得剩余的 \(2N\) 个数中前 \(N\) 个数之和与后 \(N\) 个数之和的差最大。

题目描述

$ N $ を $ 1 $ 以上の整数とします。

長さ $ 3N $ の数列 $ a = (a_1, a_2, ..., a_{3N}) $ があります。 すぬけ君は、$ a $ からちょうど $ N $ 個の要素を取り除き、残った $ 2N $ 個の要素を元の順序で並べ、長さ $ 2N $ の数列 $ a' $ を作ろうとしています。 このとき、$ a' $ のスコアを $ (a' の前半 N 要素の総和) - (a' の後半 N 要素の総和) $ と定義します。

$ a' $ のスコアの最大値を求めてください。

输入格式

入力は以下の形式で標準入力から与えられる。

$ N $ $ a_1 $ $ a_2 $ $ ... $ $ a_{3N} $

输出格式

$ a' $ のスコアの最大値を出力せよ。

样例 #1

样例输入 #1

2
3 1 4 1 5 9

样例输出 #1

1

样例 #2

样例输入 #2

1
1 2 3

样例输出 #2

-1

样例 #3

样例输入 #3

3
8 2 2 7 4 6 5 3 8

样例输出 #3

5

提示

制約

• $ 1 < = N < = 10^5 $
• $ a_i $ は整数である。
• $ 1 < = a_i < = 10^9 $

部分点

• $ 300 $ 点分のテストケースでは、$ N < = 1,000 $ が成り立つ。

Sample Explanation 1

$ a_2 $, $ a_6 $ を取り除くと、$ a' = (3, 4, 1, 5) $ となり、スコアは $ (3 + 4) - (1 + 5) = 1 $ となります。

Sample Explanation 2

例えば、$ a_1 $ を取り除くと、$ a' = (2, 3) $ となり、スコアは $ 2 - 3 = -1 $ となります。

Sample Explanation 3

例えば、$ a_2 $, $ a_3 $, $ a_9 $ を取り除くと、$ a' = (8, 7, 4, 6, 5, 3) $ となり、スコアは $ (8 + 7 + 4) - (6 + 5 + 3) = 5 $ となります。

思路

一开始想的是单调队列？结果发现是优先队列

思路来自：[ABC062D] 3N Numbers - 洛谷专栏 (luogu.com.cn)

本体我们可以把整个数列划分成两部分，取第一部分（前一段）前\(n\)大的值，第二部分（后一段）前\(n\)小的值。这样对两段分别加和，然后将两端的和作差即可。

很容易想到枚举分界线，对分界线两边的数字分别取最大值，时间复杂度\(O(n^2log\ n)\)，不可取。

枚举分界线的操作没有二分的性质，二分也不可取。

那么如果我们能够与处理好每个分界线所对应的前后两短的最大最小值，那么问题就迎刃而解了。

很显而易见，我们可以维护一个优先队列，最大值即为整个优先队列里前\(n\)大的值，维护最小值亦然，便于处理完成了。

代码整体时间复杂度：\(O(nlog\ n)\)。

注意：不开 long long 见祖宗！

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const double PI=acos(-1);
const int MAXN=3e5+10;
const ll mod=1e9+7;
const ll INF=1e9;
ll a[MAXN],q[MAXN],p[MAXN];
int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    ll n;cin>>n;
    priority_queue<ll,vector<ll>,greater<ll>>pq;
    ll sum=0;
    for(ll i=1;i<=3*n;i++){
        cin>>a[i];
        pq.push(a[i]);
        sum+=a[i];
        while(pq.size()>n)sum-=pq.top(),pq.pop();
        q[i]=sum;
    }

    priority_queue<ll>qp;
    sum=0;
    for(ll i=3*n;i>=1;i--){
        qp.push(a[i]);
        sum+=a[i];
        while(qp.size()>n)sum-=qp.top(),qp.pop();
        p[i]=sum;
    }
    ll ans=-1e18;
    for(ll i=n;i<=2*n;i++)ans=max(ans,q[i]-p[i+1]);
    cout<<ans;
    return 0;
}