ABC047

[ABC047A] キャンディーと2人の子供

题面翻译

输入三个数，如果存在其中两个数的和等于第三个数，输出Yes，不存在，输出No，强调一下，岛国的题最后输出要记得换行，否则听取WA声一片

题目描述

競プロ幼稚園に通う $ 2 $ 人の子供がキャンディーの取り合いをしています。

$ 3 $ 個のキャンディーパックがあり、それぞれのパックにはキャンディーが $ a $, $ b $, $ c $ 個入っています。

えび先生はこの $ 3 $ 個のパックを、キャンディーの個数が等しくなるように $ 2 $ 人に分けようとしています。そのような分け方が可能かどうかを判定してください。

ただし、キャンディーをパックから取り出すことはできず、それぞれのパックをそのままどちらかの子供にあげる必要があります。

输入格式

入力は以下の形式で標準入力から与えられる。

$ a $ $ b $ $ c $

输出格式

キャンディーを同じ個数に分けられるなら Yes を、そうでなければ No を出力せよ。

样例 #1

样例输入 #1

10 30 20

样例输出 #1

Yes

样例 #2

样例输入 #2

30 30 100

样例输出 #2

No

样例 #3

样例输入 #3

56 25 31

样例输出 #3

Yes

提示

制約

• $ 1 ≦ a, b, c ≦ 100 $

Sample Explanation 1

ひとりめの子供に $ 30 $ 個のキャンディーの入ったパックを、もう一方の子供に $ 10 $ 個と $ 20 $ 個のキャンディーの入ったパックをあげると、$ 2 $ 人のもらうキャンディーの個数を等しくすることができます。

Sample Explanation 2

この場合、$ 100 $ 個のキャンディーの入ったパックを貰った子供は必ずもう一方の子供より多くのキャンディーを貰うことになってしまいます。 $ 3 $ つすべてのパックをどちらかの子供にあげるように分けなければならないことに注意してください。

思路

直接模拟即可

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAXN=2e5+10;
const int mod=1e9+7;
int main(){
    ios::sync_with_stdio(false);
    int a,b,c;cin>>a>>b>>c;
    if(a+b==c||a+c==b||b+c==a)cout<<"Yes\n";
    else cout<<"No\n";
    return 0;
}

[ABC047B] すぬけ君の塗り絵 2 イージー

题面翻译

平面上有一个左下角坐标\((0,0)\)，右上角坐标\((W,H)\) 的矩形，起初长方形内部被涂白。

现在给出\(N\)个操作，每个操作都给定一个点\((x_i,y_i)\)和一个参数\(a_i\)，代表：

• \(a_i=1\)时，\(x<x_i\)的区域将被涂黑
• \(a_i=2\)时，\(x>x_i\)的区域将被涂黑
• \(a_i=3\)时，\(y<y_i\)的区域将被涂黑
• \(a_i=4\)时，\(y>y_i\)的区域将被涂黑

现在问当所有操作均结束后剩下的白色区域的面积

题目描述

$ xy $ 平面上に、左下の座標が $ (0, 0) $、右上の座標が $ (W, H) $ で、各辺が $ x $ 軸か $ y $ 軸に平行な長方形があります。最初、長方形の内部は白く塗られています。

すぬけ君はこの長方形の中に $ N $ 個の点を打ちました。$ i $ 個目 ($ 1 ≦ i ≦ N $) 点の座標は $ (x_i, y_i) $ でした。

また、すぬけ君は長さ $ N $ の数列 $ a $ を決めて、各 $ 1 ≦ i ≦ N $ に対し、

• $ a_i = 1 $ のときは長方形の $ x < x_i $ をみたす領域
• $ a_i = 2 $ のときは長方形の $ x > x_i $ をみたす領域
• $ a_i = 3 $ のときは長方形の $ y < y_i $ をみたす領域
• $ a_i = 4 $ のときは長方形の $ y > y_i $ をみたす領域

を黒く塗りました。

塗りつぶしが終わったあとの長方形内での白い部分の面積を求めてください。

输入格式

入力は以下の形式で標準入力から与えられる。

$ W $ $ H $ $ N $ $ x_1 $ $ y_1 $ $ a_1 $ $ x_2 $ $ y_2 $ $ a_2 $ $ : $ $ x_N $ $ y_N $ $ a_N $

输出格式

塗りつぶしが終わったあとの長方形内での白い部分の面積を出力せよ。

样例 #1

样例输入 #1

5 4 2
2 1 1
3 3 4

样例输出 #1

9

样例 #2

样例输入 #2

5 4 3
2 1 1
3 3 4
1 4 2

样例输出 #2

0

样例 #3

样例输入 #3

10 10 5
1 6 1
4 1 3
6 9 4
9 4 2
3 1 3

样例输出 #3

64

提示

制約

• $ 1 ≦ W, H ≦ 100 $
• $ 1 ≦ N ≦ 100 $
• $ 0 ≦ x_i ≦ W $ ($ 1 ≦ i ≦ N $)
• $ 0 ≦ y_i ≦ H $ ($ 1 ≦ i ≦ N $)
• $ W $, $ H $ (21:32 追記), $ x_i $, $ y_i $ は整数である
• $ a_i $ ($ 1 ≦ i ≦ N $) は $ 1, 2, 3, 4 $ のいずれかである

Sample Explanation 1

すぬけ君が塗りつぶしを始める前の長方形は以下の図のようになっています。 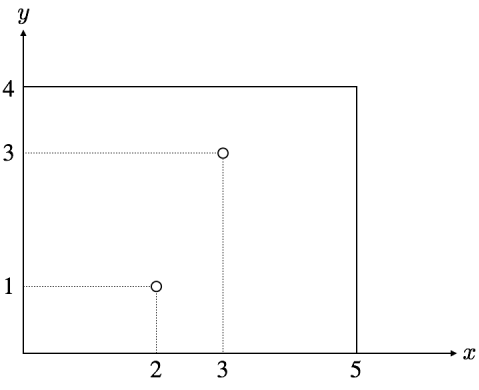 $ (x_1, y_1) = (2, 1) \(、\) a_1 = 1 $ なので、まずすぬけ君は $ x $ 座標が $ 2 $ より小さい領域を塗りつぶし、長方形は以下のようになります。 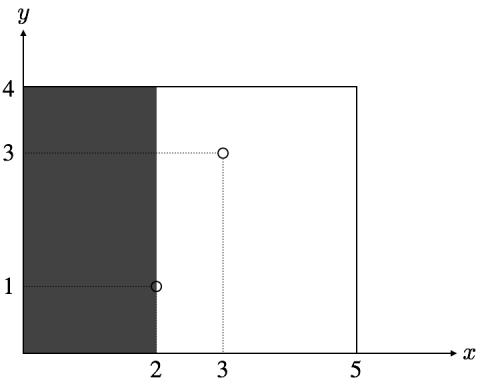 $ (x_2, y_2) = (3, 3) \(、\) a_2 = 4 $ なので、次にすぬけ君は $ y $ 座標が $ 3 $ より大きい領域を塗りつぶし、長方形は最終的に以下のようになります。  この最終的な状態における白い部分の面積は $ 9 $ なので、出力は $ 9 $ となります。

Sample Explanation 2

塗りつぶした結果、白い部分が残らないこともありえます。

思路

其实直接暴力就可以，但是我们想想优化方法

以\(a=1\)为例，可以发现：对结果有影响的只有当\(a=1\)时，所有\(x\)的可能取值中最大的，其他的只是重复填涂而已，对结果没影响。同理可得\(a=2,a=3,a=4\)的情况。

注意可能是否不存在的情况

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAXN=2e5+10;
const int mod=1e9+7;
int m[110][110];
int main(){
    ios::sync_with_stdio(false);
    int w,h,n;cin>>w>>h>>n;
    int a1=0,a2=w,a3=0,a4=h;
    for(int i=1;i<=n;i++){
        int x,y,a;cin>>x>>y>>a;
        if(a==1){
            a1=max(a1,x);
        }
        if(a==2){
            a2=min(a2,x);
        }
        if(a==3){
            a3=max(a3,y);
        }
        if(a==4){
            a4=min(a4,y);
        }
    }
    //如果右边界小于左边界，或者上边界小于下边界
    if(a4<a3||a2<a1){
        cout<<0;
    }
    else cout<<(a2-a1)*(a4-a3);
    return 0;
}

[ABC047C] 一次元リバーシ

题面翻译

输入一个长度不多于\(10^5\)的字符串，只包含B或W。若前后两个字符不一样，答案累加，输出答案。

感谢@da32s1da 提供的翻译

题目描述

きつねの次郎と三郎が一次元リバーシで遊んでいます。一次元リバーシでは、盤面には白か黒の石が一列に並んだ状態となっており、列の右端か左端に新たに石を打っていきます。通常のリバーシと同じように、たとえば白の石を打つことで黒の石を挟むと、挟まれた黒の石は白い石に変わります。

ゲームの途中で三郎に急用ができて帰ってしまうことになりました。このとき、盤面の状態は文字列 $ S $ で表されます。石は $ |S| $ (文字列の長さ) 個並んでおり、左から $ i $ ($ 1 ≦ i ≦ |S| \() 個目の石の色は、\) S $ の $ i $ 文字目が B のとき黒、W のとき白です。

次郎は現在の盤面に対して、できるだけ少ない個数の石を新たに打つことで全ての石を同じ色にしようと考えました。最小で何個の石を打てばよいかを求めてください。

输入格式

入力は以下の形式で標準入力から与えられる。

$ S $

输出格式

全ての石を同じ色にするために打つ必要のある石の個数の最小値を出力せよ。

样例 #1

样例输入 #1

BBBWW

样例输出 #1

1

样例 #2

样例输入 #2

WWWWWW

样例输出 #2

0

样例 #3

样例输入 #3

WBWBWBWBWB

样例输出 #3

9

提示

制約

• $ 1 ≦ |S| ≦ 10^5 $
• $ S $ に含まれる文字は B または W のいずれかである

Sample Explanation 1

たとえば右端に黒い石を打つとすべての白い石を黒い石にすることができます。他にも、左端に白い石を打つことでもすべての石の色を同じにできます。 いずれの場合も $ 1 $ 個の石ですべての石を同じ色にすることができるので、$ 1 $ を出力します。

Sample Explanation 2

最初から全ての石が同じ色の場合、新たに石を打つ必要はありません。

思路

开个\(flag\)记录一下即可

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAXN=2e5+10;
const int mod=1e9+7;
int m[110][110];
int main(){
    ios::sync_with_stdio(false);
    string s;cin>>s;
    char flag=s[0];
    int ans=0;
    for(int i=1;i<s.length();i++){
        if(flag!=s[i]){
            ans++;
            flag=s[i];
        }
        if(s[i]!=s[i-1]){
            flag=s[i];
        }
    }
    cout<<ans;
    return 0;
}

---

发现自己\(SB\)了，直接统计有多少个相邻的字符不同即可

[ABC047D] 高橋君と見えざる手

题面翻译

高桥君和不可见之手

问题描述

有 \(N\) 个小镇排在一条直线上。旅行商人高桥君从小镇 \(1\) 出发，一边买卖苹果一边朝小镇 \(N\) 前行。

开始时高桥君处在小镇 \(1\) ，身上一个苹果也没有。高桥君不断进行以下行动。

• 移动：从小镇 \(i(i < N)\) 开始，移动到小镇 \(i+1\) 。
• 买卖苹果：买进或卖出任意个苹果。在小镇 \(i(1 \leq i \leq N)\) 买进或卖出苹果单价都为 \(A_i\) 円。 \(A_i\) 为相异的整数。

在每个小镇进行交易的苹果数量没有限制，但是旅行中所买进和卖出的苹果总数(买进苹果数加上卖出苹果数)必须在 \(T\) 以内。高桥君会使自己在旅程中所获利益(卖苹果所得钱数减去买苹果所花钱数)最大。

在高桥君进行旅行之前，青木君可以对于任意 \(i\) ，使 \(A_i\) 变为非负整数 \(A_i'\) 。这个操作的代价为 \(|A_i-A_i'|\) 。操作后即使出现相异小镇苹果单价相同的情况也没关系。

青木君的目的是：花费尽量少的代价，使高桥君所得的最大利益至少下降 \(1\) 円。请求出最小代价。

数据保证初始状态下高桥君至少能获得 \(1\) 円的利益。

数据范围

• \(1 \leq N \leq 10^5\)
• \(1 \leq A_i \leq 10^9\)
• \(A_i\) 相异
• \(2 \leq T \leq 10^9\)
• 保证初始状态下高桥君至少能获得 \(1\) 円的利益。

输入

输入按以下标准： \[ N \space T \] \[ A_1 \space A_2 \space \dots \space A_N \]

输出

输出使高桥君最大收益至少下降 \(1\) 円的最小代价和。

样例1解释

在初始状态下，高桥君能够进行以下的行动来获得最大收益( \(150\) 円)：

1. 从小镇 \(1\) 移动到小镇 \(2\) 。
2. 在小镇 \(2\) 处花 \(50\) 円买一个苹果。
3. 从小镇 \(2\) 移动到小镇 \(3\) 。
4. 在小镇 \(3\) 处卖掉一个苹果获得 \(200\) 円。

举例来说，如果青木君把小镇 \(2\) 的苹果单价从 \(50\) 円上调至 \(51\) 円，高桥君就无法获得 \(150\) 円的收益。也就是说，此操作能够使高桥君的最大收益至少下降 \(1\) 円，所以答案为 \(1\) 。

另外，将小镇 \(3\) 的苹果单价从 \(200\) 円降至 \(199\) 円也能够达到目的。

题目描述

$ N $ 個の町が一直線上に並んでいます。行商人の高橋君は町 $ 1 $ から出発し、リンゴの売買をしながら町 $ N $ へと向かいます。

はじめ高橋君は町 $ 1 $ におり、リンゴを $ 1 $ つも持っていません。高橋君は次のいずれかの行動を繰り返し行います。

• 移動: 町 $ i $ ($ i < N $) にいるとき、町 $ i + 1 $ へ移動する。
• リンゴの売買: リンゴを好きな個数だけ売買する。ここで、町 $ i $ ($ 1 ≦ i ≦ N $) ではリンゴの買値も売値もともに $ A_i $ 円とする。ここで $ A_i $ は相異なる整数です。

$ 1 $ つの町で売買するリンゴの個数に制限はありませんが、旅の中で売買するリンゴの個数は合計で (買う個数と売る個数を合わせて) $ T $ 個以下にしなくてはなりません。

高橋君は旅の利益、すなわちリンゴを売った代金から買った代金を引いた値を最大にするように旅をするとします。旅が終わったときに持っていたリンゴの価値は考えず、旅の中で売買した金額だけを考えます。

この旅に先立って、青木君は任意の町 $ i $ に対して $ A_i $ を好きな非負整数 $ A_i' $ に変えるという操作を好きなだけ行うことができます。ただし、この操作は行うごとに $ |A_i - A_i'| $ のコストがかかります。操作後には異なる町の間でリンゴの値段が同じになっていても構いません。

青木君の目的はできるだけ少ない合計コストの操作で高橋君の利益を少なくとも $ 1 $ 円下げることです。合計コストの最小値を求めてください。

ただし、元の状態で高橋君が $ 1 $ 円以上の利益を上げられることは仮定して構いません。

输入格式

入力は以下の形式で標準入力から与えられる。

$ N $ $ T $ $ A_1 $ $ A_2 $ $ ... $ $ A_N $

输出格式

高橋君の収益を少なくとも $ 1 $ 円下げるために必要な合計コストの最小値を出力せよ。

样例 #1

样例输入 #1

3 2
100 50 200

样例输出 #1

1

样例 #2

样例输入 #2

5 8
50 30 40 10 20

样例输出 #2

2

样例 #3

样例输入 #3

10 100
7 10 4 5 9 3 6 8 2 1

样例输出 #3

2

提示

制約

• $ 1 ≦ N ≦ 10^5 $
• $ 1 ≦ A_i ≦ 10^9 $ ($ 1 ≦ i ≦ N $)
• $ A_i $ は相異なる
• $ 2 ≦ T ≦ 10^9 $
• 入力の状態では高橋君は $ 1 $ 円以上の利益を上げられることが保証される

Sample Explanation 1

この入力の状態では、高橋君は次のようにして最大の利益である $ 150 $ 円を達成することができます。 1. 町 $ 1 $ から町 $ 2 $ へ移動する。 2. 町 $ 2 $ で $ 50 $ 円を支払い、リンゴを $ 1 $ 個買う。 3. 町 $ 2 $ から町 $ 3 $ へ移動する。 4. 町 $ 3 $ で $ 200 $ 円でリンゴを $ 1 $ 個売る。 たとえば、青木君が町 $ 2 $ のリンゴの値段を $ 50 $ 円から $ 51 $ 円に変えると、高橋君はどのようにしても $ 150 $ 円の利益を上げることができなくなります。すなわち、コスト $ 1 $ で高橋君の利益を少なくとも $ 1 $ 円下げることが可能であり、答えは $ 1 $ となります。 他にも、町 $ 3 $ のリンゴの値段を $ 200 $ 円から $ 199 $ 円に変えることでもコスト $ 1 $ で高橋君の利益を下げることが可能です。

思路

高木的理想情况就是最高售价-最低买价（记作\(MAX\)），那么我们只需要找到所有的满足情况即可。

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int MAXN=1e5+10;
const int mod=1e9+7;
ll b[MAXN];
int main(){
    ios::sync_with_stdio(false);
    ll n,t;cin>>n>>t;
    ll MAX=LONG_LONG_MIN,MIN=LONG_LONG_MAX;
    for(int i=1;i<=n;i++){
        ll a;cin>>a;
        //b记录的是该方案对应的利润
        b[i]=a-MIN;
        //MIN：最低购入价格
        MIN=min(MIN,a);
        //MAX最大利润
        MAX=max(MAX,b[i]);
    }
    ll ans=0;
    for(int i=1;i<=n;i++){
        if(b[i]==MAX)ans++;
    }
    cout<<ans;
    return 0;
}