ABC054
ABC054
[ABC054B] Template Matching
题面翻译
给与纵N行,横N N列像素排列了的图像A,纵M行,横M M列像素排列了的模板图像B。
像素是构成图像的最小单位,其中1×1×1的正方形。
另外,给定的图像全部是二值图像,各像素的颜色用白和黑两种表示。
在输入中,全部的像素用文字表示,.白色的像素,#与黑色的像素对应。图像A由N N个字符串A_1、...、A_N A 1、...、A_N A N表示。字符串A_i Ai
的j j字符目对应于图像A上第i i、从左边第j j j个像素。(1≤i,j≤N) (1≤i,j≤N)同样,模板图像B由M M个字符串B_1,...,B_M B 1,...,B M M M表示。字符串B_i B i的j j j字符目对应于模板图像B上第i i、从左边第j j j的像素。(1≤i,j≤M) (1≤i,j≤M)
当仅允许图像平行移动时,请确定模板图像B是否包含在图像A中。
题目描述
縦 $ N $ 行、横 $ N $ 列に画素が並んだ画像Aと、縦 $ M $ 行、横 $ M $ 列に画素が並んだテンプレート画像Bが与えられます。
画素は画像を構成する最小単位であり、ここでは $ 1×1 $ の正方形とします。
また、与えられる画像は全て2値画像であり、各画素の色は白と黒の2種類で表されます。入力において、全ての画素は文字で表されており、
.は白色の画素、#は黒色の画素に対応します。
画像Aは $ N $ 個の文字列 $ A_1,...,A_N $ で表されます。
文字列 $ A_i $ の $ j $ 文字目は、画像Aの上から $ i $ 番目、左から $ j $ 番目の画素に対応します。$ (1≦i,j≦N) $
同様に、テンプレート画像Bは $ M $ 個の文字列 $ B_1,...,B_M $ で表されます。
文字列 $ B_i $ の $ j $ 文字目は、テンプレート画像Bの上から $ i $ 番目、左から $ j $ 番目の画素に対応します。$ (1≦i,j≦M) $画像の平行移動のみ許されるとき、テンプレート画像Bが画像Aの中に含まれているかを判定してください。
输入格式
入力は以下の形式で標準入力から与えられる。
$ N $ $ M $ $ A_1 $ $ A_2 $ $ : $ $ A_N $ $ B_1 $ $ B_2 $ $ : $ $ B_M $
输出格式
画像Aの中にテンプレート画像Bを含む場合は
Yes、含まない場合はNoを出力せよ。样例 #1
样例输入 #1
#.#
.#.
#.#
#.
.#样例输出 #1
样例 #2
样例输入 #2
....
....
....
....
#样例输出 #2
提示
制約
- $ 1≦M≦N≦50 $
- $ A_i $ は
#と.からなる長さ $ N $ の文字列- $ B_i $ は
#と.からなる長さ $ M $ の文字列Sample Explanation 1
テンプレート画像Bが、画像A中の左上の $ 2 × 2 $ の部分画像と右下の $ 2 × 2 $ の部分画像に一致するため、
Yesと出力します。Sample Explanation 2
画像Aは白色の画素、テンプレート画像Bは黒色の画素で構成されるため、含まれることはありません。
思路
直接从矩形的左上角开始暴力匹配即可
|
[ABC054C] One-stroke Path
题面翻译
题目描述
给定一个没有重边和自环的 \(N\) 个点 \(M\) 条边的无权无向图,第 \(i\) 条边连接顶点 \(a _ i\) 和 \(b _ i\)。
求以顶点 \(1\) 为起点,只访问 \(1\) 次所有顶点的路径有多少条?特别地,起点和终点也视为被访问。
输入格式
第一行两个整数 \(N, M\)。
接下来 \(m\) 行,其中第 \(i\) 行两个整数 \(a _ i, b _ i\)。
$ N M \ a _ 1 b _ 1 \ a _ 2 b _ 2 \ \ a _ M b _ M $
输出格式
输出满足条件的路径有多少。
数据范围
$ 2 N \ 0 M N(N - 1) \ 1 a _ i < b _ i N $
给定的无向图中不包含重边和自环。
题目描述
自己ループと二重辺を含まない $ N $ 頂点 $ M $ 辺の重み無し無向グラフが与えられます。
$ i (1≦i≦M) $ 番目の辺は頂点 $ a_i $ と頂点 $ b_i $ を結びます。
ここで、自己ループは $ a_i = b_i (1≦i≦M) $ となる辺のことを表します。
また、二重辺は $ a_i=a_j $ かつ $ b_i=b_j (1≦i < j≦M) $ となる辺のことを表します。
頂点 $ 1 $ を始点として、全ての頂点を1度だけ訪れるパスは何通りありますか。
ただし、パスの始点と終点の頂点も訪れたものとみなします。例として、図1のような無向グラフが与えられたとします。
図1:無向グラフの例
このとき、図2で表されるパスは条件を満たします。
図2:条件を満たすパスの例
しかし、図3で表されるパスは条件を満たしません。全ての頂点を訪れていないからです。
図3:条件を満たさないパスの例1
また、図4で表されるパスも条件を満たしません。始点が頂点 $ 1 $ ではないからです。
図4:条件を満たさないパスの例2
输入格式
入力は以下の形式で標準入力から与えられる。
$ N $ $ M $ $ a_1 $ $ b_1 $ $ a_2 $ $ b_2 $ $ : $ $ a_M $ $ b_M $
输出格式
問題文の条件を満たすパスが何通りあるか出力せよ。
样例 #1
样例输入 #1
1 2
1 3
2 3样例输出 #1
样例 #2
样例输入 #2
1 3
2 7
3 4
4 5
4 6
5 6
6 7样例输出 #2
提示
制約
- $ 2≦N≦8 $
- $ 0≦M≦N(N-1)/2 $
- $ 1≦a_i < b_i≦N $
- 与えられるグラフは自己ループと二重辺を含まない。
Sample Explanation 1
与えられるグラフは以下の図で表されます。 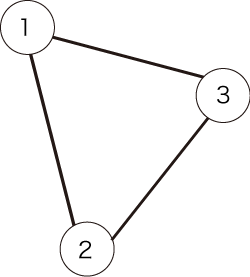 条件を満たすパスは以下の $ 2 $ 通りです。 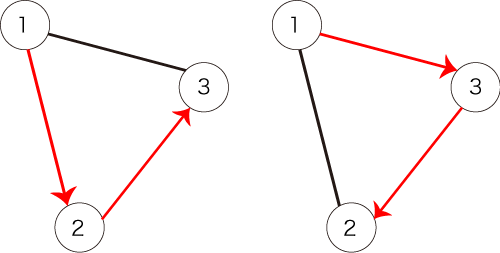
Sample Explanation 2
このテストケースは問題文の例と同じです。
思路
范围很小,直接DFS即可,记录从1开始能否访问所有顶点的路径数。
|
[ABC054D] Mixing Experiment
题面翻译
题目描述:
有 \(N\) 个物体,第 \(i\) 个物体含有 \(a_i\) 质量的 A 元素 和 \(b_i\) 质量的 B 元素,代价为 \(c_i\) 。
问能否取若干个物体,使 A 元素与 B 元素质量之比为 \(M_a : M_b\) ,并使代价最小。
输入格式:
第一行3个整数 \(N ,M_a ,M_b\)
下面 \(N\) 行,每行3个整数 \(a_i ,b_i ,c_i\)
$ N $ $ M_a $ $ M_b $
$ a_1 $ $ b_1 $ $ c_1 $
$ a_2 $ $ b_2 $ $ c_2 $$ : $
$ a_N $ $ b_N $ $ c_N $
输出格式:
若能满足条件则输出 最小代价。
否则输出 -1
数据范围:
\(1\le N\le 40\)
\(1\le a_i,b_i\le 10\)
\(1\le c_i\le 100\)
\(1\le M_a,M_b\le 10\)
\(gcd(M_a,M_b)=1\)
输入都为整数。
translated by @君のNOIP。
题目描述
イルカは、微量の物質Cを生成したいと考えています。
物質Cを生成するためには、タイプAの物質とタイプBの物質の混合比が $ M_a:M_b $ となる溶液を用意する必要があります。
しかし、イルカは薬品を1つも持っていないため、薬局へ薬品を買いに行くことにしました。
薬局では、$ N $ 種類の薬品を取り扱っており、各薬品 $ i $ の在庫はちょうど1つです。
各薬品 $ i $ は、タイプAの物質 $ a_i $ グラム、タイプBの物質 $ b_i $ グラム含んでおり、価格 $ c_i $ 円で売られています。
イルカは、いくつかの薬品を薬局で買います。買った薬品は全て使わなければなりません。
物質Cを生成するために、必要な最小予算を求めてください。
薬局で売られている薬品の組み合わせで、物質Cを生成できない場合はそれを報告してください。输入格式
入力は以下の形式で標準入力から与えられる。
$ N $ $ M_a $ $ M_b $ $ a_1 $ $ b_1 $ $ c_1 $ $ a_2 $ $ b_2 $ $ c_2 $ $ : $ $ a_N $ $ b_N $ $ c_N $
输出格式
物質Cを生成するために必要な最小予算を出力せよ。物質Cを生成できない場合には
-1を出力せよ。样例 #1
样例输入 #1
1 2 1
2 1 2
3 3 10样例输出 #1
样例 #2
样例输入 #2
10 10 10样例输出 #2
提示
制約
- $ 1≦N≦40 $
- $ 1≦a_i,b_i≦10 $
- $ 1≦c_i≦100 $
- $ 1≦M_a,M_b≦10 $
- $ gcd(M_a,M_b)=1 $
- $ a_i \(、\) b_i \(、\) c_i \(、\) M_a \(、\) M_b $は整数である。
Sample Explanation 1
最小予算となる組み合わせは、薬品 $ 1 $ と薬品 $ 2 $ を混合する場合です。 この場合、混合した溶液中に物質Aは $ 3 $ グラム、物質Bは $ 3 $ グラム含まれており、混合比は $ 3:3=1:1 $ となって条件を満たします。 このときの合計価格は $ 3 $ 円となります。
Sample Explanation 2
物質Aと物質Bの混合比が $ 1:10 $ となる薬品の組み合わせはないので、
-1を出力します。
思路
很容易看出来这是一个01背包问题。
注意有两个维度:\(dp[i][j]\)表示\(A\)总质量为\(i\),\(B\)总质量为\(j\)。由此可得状态转移方程,注意要倒序枚举。
|

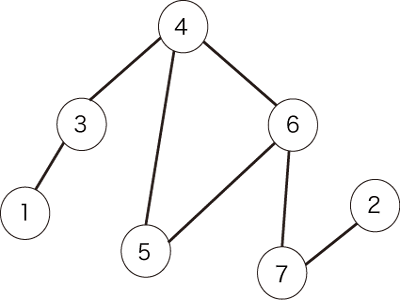 図1:無向グラフの例
図1:無向グラフの例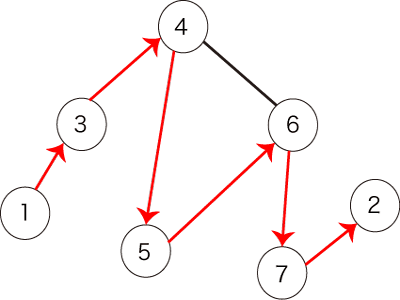 図2:条件を満たすパスの例
図2:条件を満たすパスの例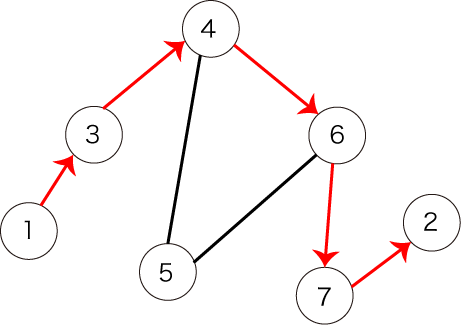 図3:条件を満たさないパスの例1
図3:条件を満たさないパスの例1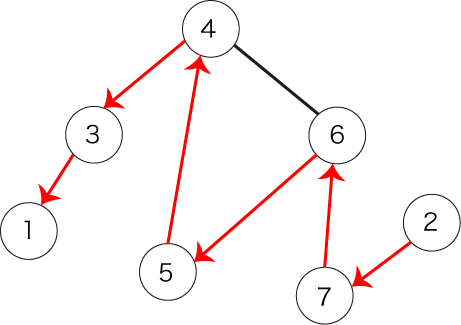 図4:条件を満たさないパスの例2
図4:条件を満たさないパスの例2




