SCUT2007 Data Structure
SCUT2007
Select the correct choice.
- An algorithm must be or do all of the following EXCEPT: ( D )
- Correct(正确的)
- Finite(有限的)
- Terminate(终止的)
- Ambiguous(模糊)
答案解释:
- 选项 A:算法必须是正确的(Correct),意味着它能够按照既定的目标准确地处理输入,并输出符合预期要求的结果,这是算法有效性的基本保障。
- 选项 B:算法必须是有限的(Finite),即它在执行过程中经过有限的步骤后就能够结束运行,不能无限制地持续运行下去,否则无法实际应用。
- 选项 C:算法要能终止(Terminate),这与有限性密切相关,强调算法最终会完成并输出相应结果,不会陷入无限循环等无法结束的状态。
- 选项 D:算法绝不能是模糊的(Ambiguous),其每一步操作、执行逻辑以及相应的处理规则都应当清晰明确,这样才能保证对于相同的输入总是能得到一致的输出,所以算法不应具备模糊性这一特性,本题选 D。
- Pick the growth rate(增长率) that corresponds to the most
efficient(有效率的) algorithm as \(n\) gets large: ( C )
- \(n!\)
- \(2^n\)
- \(10n\log n\)
- \(2n^2\)
答案解释:
- 选项 A:\(n!\) 的增长速度极快,随着 \(n\) 的增大,其数值会呈现出急剧上升的趋势。例如,当 \(n = 5\) 时,\(5! = 120\);当 \(n = 6\) 时,\(6! = 720\)。这种增长速度意味着对应的算法复杂度很高,效率较低,不适合处理大规模的数据。
- 选项 B:\(2^n\) 属于指数级增长,随着 \(n\) 的不断增大,其计算量会以极快的速度膨胀。比如,当 \(n = 10\) 时,\(2^{10} = 1024\)。指数级增长的复杂度使得算法在处理大量数据时效率低下。
- 选项 C:\(10n\log n\) 的增长速度相对较为缓慢,当 \(n\) 变得很大时,相较于其他几个复杂度函数,其计算量的增加幅度相对较小。在许多高效的算法中,例如归并排序等在平均情况下复杂度接近这个量级,所以它代表着相对高效的算法,本题选 C。
- 选项 D:\(2n^2\) 是多项式级增长,其增长速度比线性增长快,随着 \(n\) 的增大,计算量也会明显增多,没有 \(10n\log n\) 对应的算法效率高。
- If a data element requires 6 bytes and a pointer requires 4 bytes,
then a linked list representation will be more space efficient than a
standard array representation when the fraction of non-null elements is
less than about: ( B )
- \(\frac{2}{3}\)
- \(\frac{3}{5}\)
- \(\frac{3}{4}\)
- \(\frac{1}{2}\)
答案解释: 设总元素个数为 \(n\),每个数据元素占 \(6\) 字节,则标准数组总空间 \(S_{array}=6n\) 字节。
对于链表,每个节点由 \(6\) 字节的数据元素和 \(4\) 字节的指针组成,即每个节点共占用 \(10\) 字节。若非空元素个数为 \(m\),则链表总空间 \(S_{list}=10m\) 字节。
当链表比数组更节省空间时,需满足 \(S_{list}<S_{array}\),即:
\[ \begin{align*} 10m &< 6n\\ \frac{m}{n} &< \frac{6}{10}\\ \frac{m}{n} &< \frac{3}{5} \end{align*} \]
这意味着当非空元素所占比例小于 \(\frac{3}{5}\) 时,链表在空间利用上相较于标准数组更高效,所以选 B。
- Which statement is not correct among the following
four(下面那个描述是不正确的): ( A )
- The worst case for my algorithm is \(n\) becoming larger and larger because that is the slowest.
- A cluster(簇) is the smallest unit of allocation(分配) for a file, so all files occupy(占据) a multiple(倍数) of the cluster size.(没有学过的知识点)
- The selection sort is an unstable(不稳定的) sorting algorithm.
- The number of leaves in a non-empty full binary tree is one more than the number of internal nodes.
答案解释:
- 选项 A:算法的最坏情况是指在所有可能的输入情况中,导致算法执行时间最长或者资源消耗最多的特定情形。但并不是简单地随着输入规模 \(n\) 越来越大就一定是最坏情况,最坏情况往往取决于输入数据的具体分布、结构以及算法自身的特点等多种因素,所以该说法不准确,本题选 A。
- 选项 B:簇(cluster)确实是文件在磁盘上分配存储空间的最小单元,文件所占用的磁盘空间必然是簇大小的整数倍,这是磁盘存储文件的基本特性之一,该说法正确。
- 选项 C:选择排序(Selection sort)是不稳定的排序算法。在排序过程中,若存在相等元素,由于选择排序会通过交换操作来调整元素位置,可能会改变相等元素原本的相对顺序,所以它不具备稳定性,该说法正确。
- 选项 D:对于非空满二叉树,其叶子节点数 \(L\) 和内部节点数 \(I\) 满足关系 \(L = I + 1\),这是满二叉树的一个重要性质,该说法正确。
- Which of the following is a true statement: ( C )
- In a BST, the left child of any node is less than the right child, and in a heap, the left child of any node is less than the right child.
- In a BST, the left child of any node could be less or greater than the right child, but in a heap, the left child of any node must be less than the right child.
- In a BST, the left child of any node is less than the right child, but in a heap, the left child of any node could be less than or greater than the right child.
- In both a BST and a heap, the left child of any node could be either less than or greater than the right child.
答案解释:
- 二叉搜索树(BST):其定义的性质决定了左子树的所有节点值小于根节点值,根节点值小于右子树的所有节点值,也就是任意节点的左孩子节点的值必然小于右孩子节点的值。
- 堆(heap):以最大堆为例,它只保证父节点的值大于等于(大顶堆情况)其左右子节点的值,但对于左右子节点之间并没有严格规定左孩子一定小于或大于右孩子,左右子节点的大小关系是相对灵活的,只要它们都小于等于父节点即可。所以选项 C 的描述准确地体现了这两种数据结构关于节点值比较的特点。
- The most effective way to reduce the time required by a disk-based
program is to: ( B )
- Improve the basic operations.
- Minimize the number of disk accesses.
- Eliminate the recursive calls.
- Reduce main memory use.
答案解释:
- 选项 A:改进基本操作虽然可能在一定程度上提高程序的运行效率,但对于基于磁盘的程序而言,磁盘访问速度相对内存操作速度要慢得多,磁盘访问的开销往往是整个程序运行时间的瓶颈所在,所以改进基本操作并非最有效的办法。
- 选项 B:由于磁盘读写速度远远低于内存操作速度,所以尽可能减少磁盘访问的次数,能够极大地降低程序因等待磁盘读写而耗费的时间,这对于减少磁盘程序的运行时间是最为关键和有效的途径,本题选 B。
- 选项 C:消除递归调用可能会优化程序的栈空间使用情况或者部分执行流程,但对于磁盘程序的运行时间来说,它并非是最主要的影响因素,重点还是在于对磁盘读写相关的优化。
- 选项 D:减少主内存使用对磁盘程序运行时间的影响并不大,磁盘程序的性能关键在于磁盘与内存之间的数据交互效率,尤其是磁盘访问次数等方面的优化。
- The max-heap constructed by a sequence of key (46, 79, 56, 38, 40,
84) is ( )?
- 79, 46, 56, 38, 40, 84
- 84, 79, 56, 46, 40, 38
- 84, 79, 46, 38, 40, 56
- 84, 56, 79, 40, 46, 38
答案解释: 构建最大堆(max - heap)的过程是从最后一个非叶子节点开始,依次对每个非叶子节点进行调整,使其满足最大堆的性质(父节点值大于等于子节点值)。
对于给定的序列\((46, 79, 56, 38, 40, 84)\): 首先根据完全二叉树节点编号与数组下标的对应关系,找到最后一个非叶子节点(\(n/2\)向下取整对应的节点,\(n\) 为节点总数,这里 \(n = 6\),最后一个非叶子节点是索引为 \(2\) 的节点,对应值 \(56\)),然后依次向前调整节点。
经过相应的调整操作后,得到的最大堆为\((84, 79, 56, 38, 40, 46)\),该结构满足父节点值大于子节点值的最大堆性质,没有正确选项。
- If there is 0.5MB working memory, 4KB blocks, yield 128
blocks for working memory. By the multi-way merge in external sorting,
the average run size and the sorted size in one pass of multi-way merge
on average are separately ( A )?(这题不懂,重点关注)
- 1MB, 128MB
- 1MB, 64MB
- 2MB, 64 MB
- 0.5 MB, 128MB
答案解释: 已知工作内存为 \(0.5MB\),块大小为 \(4KB\),因为 \(1MB = 1024KB\),所以工作内存包含的块数为:
\[ \frac{0.5 \times 1024KB}{4KB} = 128 \text{ 块} \]
在多路归并外部排序中:
- 平均归并段大小:由于每次可以利用工作内存中的所有块读入数据来形成归并段,所以平均归并段大小就等于工作内存的大小,即 \(1MB\)(\(128 \times 4KB = 1MB\))。
- 一趟多路归并后排序好的数据大小:一趟多路归并能够处理的就是所有归并段的数据,已知归并段大小为 \(1MB\),且一共有 \(128\) 个归并段参与合并,那么一趟归并后排序好的数据大小为 \(128MB\),所以选 A。
- Tree indexing methods are meant to overcome what
deficiency in hashing? ( D )
- Inability to handle range queries.
- Inability to maximum queries
- Inability to handle queries in key order
- All of above.
答案解释:
- 选项 A:哈希表在处理范围查询时存在明显困难,例如要查询某个连续范围内的键值对应的记录,哈希表难以直接高效地支持这种按范围筛选数据的操作,而树索引(如 B 树等)可以借助节点之间的有序关系方便地处理范围查询。
- 选项 B:哈希表本身很难直接高效地进行求最大值这类查询操作,它主要是通过键快速定位对应的值,缺乏像树结构那样基于有序性方便地查找最值的特性,树索引则可以依据其节点顺序便捷地找到最大值等。
- 选项 C:哈希表是依据哈希函数将键打乱顺序进行存储的,不能方便地按照键的顺序来处理查询任务,而树索引天然具备节点之间的顺序关系,便于按照键顺序进行查询操作。
综上所述,树索引方法旨在克服哈希表上述所有这些不足之处,本题选 D。
- Assume that we have eight records, with key values A to H,
and that they are initially placed in alphabetical order. Now, consider
the result of applying the following access pattern: E D F G B G F A F E
G B, if the list is organized by the move-to-front heuristic, then the
final list will be ( B ).(没有学习过的知识点)
- B G E F D A C H
- B G E F A D C H
- A B F D G E C H
- F D G E A B C H
答案解释: 按照移至前端(move-to-front)启发式策略来处理访问序列 \(E D F G B G F A F E G B\) : 初始顺序为 \(A B C D E F G H\)(按字母顺序排列)。 当访问 \(E\) 时,将 \(E\) 移到最前面,此时序列变为 \(E A B C D F G H\)。 接着访问 \(D\) 时,把 \(D\) 移到最前面,序列变为 \(D E A B C F G H\),以此类推,根据每次访问元素都将其移到列表最前端的规则,处理完整个访问序列后,最终得到的列表是 \(B G E F A D C H\),所以选 B。
Fill the blank with correct C++ codes
(1)Given an array storing integers ordered by value, modify the binary search routines to return the position of the first integer with the greatest value less than K when K itself does not appear in the array. Return ERROR if the least value in the array is greater than K: (10 scores)
// Return position of greatest element <= K |
更像是二分查找,注意这种二分查找的写法,最后查找到的元素是l对应的元素。
答案解释:
int i = (l + r) / 2;:这行代码的目的是取当前查找区间(由l和r界定)的中间位置索引。在二分查找中,每次迭代都通过查看中间元素来决定下一步是在左半区间还是右半区间继续查找,所以需要计算出这个中间位置的索引值,以便后续比较中间元素与目标值K的大小关系,进而缩小查找范围。r = i;:当发现K < array[i]时,意味着目标值K在当前中间元素array[i]的左边区间,此时需要更新查找区间的右边界r,将其设置为当前中间位置i,这样下一次迭代就会在左半区间继续查找,缩小查找范围以找到符合要求(小于等于K的最大元素)的元素。return i;:如果发现K == array[i],说明找到了与目标值K相等的元素,按照题目要求,直接返回该元素所在的位置索引i,因为它就是符合条件(等于K也算满足小于等于K)的元素位置。l = i;:当K > array[i]时,表明目标值K在当前中间元素array[i]的右边区间,这时要更新查找区间的左边界l,将其设置为当前中间位置i,下一次迭代就在右半区间继续查找,逐步逼近小于等于K的最大元素所在位置。return l;:当循环结束后(即l + 1 == r时),此时l指向的就是小于K的最大元素位置(如果存在的话),或者在没有找到符合要求的元素(比如数组中最小元素都大于K,此时l会保持初始值-1)的情况下,按照题目要求返回这个位置索引l,用于表示查找结果。
- A full 5-ary tree with 100 internal vertices has 501 vertices. ( 3 scores)
答案解释: 对于一棵满 m 叉树(这里
m = 5),其顶点总数 N 和内部顶点数
I
之间存在这样的关系:N = m * I + 1。这是因为在满
m 叉树中,每个内部节点都有 m
个孩子节点,再加上根节点(共 1
个)就构成了整棵树的顶点总数。已知内部顶点数
I = 100,根据上述公式可得顶点总数
N = 5 * 100 + 1 = 501,所以该满 5 叉树有
501 个顶点。
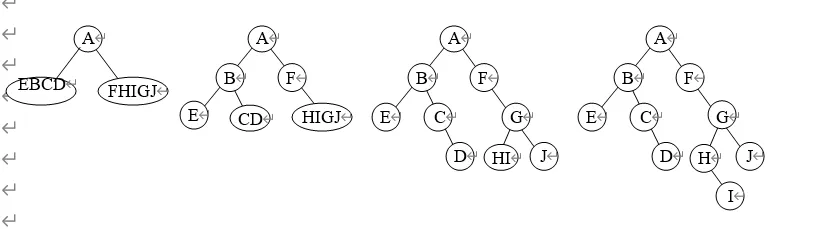
A certain binary tree has the preorder enumeration as ABECDFGHIJ and the inorder enumeration as EBCDAFHIGJ. Try to draw the binary tree and give the postorder enumeration. (The process of your solution is required!!!)
答案:Postorder enumeration: EDCBIHJGFA
答案解释:
以下是通过先序遍历和中序遍历结果来构建二叉树并得出后序遍历结果的详细过程:
1. 确定根节点
先序遍历的顺序是“根左右”,所以先序遍历序列 ABECDFGHIJ
中的第一个节点 A 就是二叉树的根节点。
2. 划分左右子树
根据中序遍历“左根右”的顺序(中序遍历序列为
EBCDAFHIGJ),在中序遍历中找到根节点 A,那么
A 左边的节点 EBCD 就是根节点 A
的左子树节点,A 右边的节点 FHIGJ 就是根节点
A 的右子树节点。
3. 进一步分析左子树
- 左子树的根节点:在先序遍历中,左子树的节点顺序是
BECD,所以左子树的根节点是B(因为先序先访问根)。 - 确定左子树的左右子树:再看中序遍历中左子树部分
EBCD,可以知道B的左子树是E,右子树节点是CD。回到先序遍历中左子树的剩余部分ECD,可知C是B的右子树的根节点,再看中序遍历EBCD里C的左右情况,可得C的左子树是D,右子树为空。
4. 进一步分析右子树
- 右子树的根节点:在先序遍历中右子树的节点顺序是
FGHIJ,所以右子树的根节点是F。 - 确定右子树的左右子树:看中序遍历右子树部分
HIGJ,可以知道F的左子树为空,右子树节点是HIGJ。再看先序遍历右子树剩余部分GHIJ,可得G是F的右子树的根节点,然后看中序遍历HIGJ里G的左右情况,可知G的左子树是HI,右子树是J。继续分析G的左子树,根据先序遍历HI可知H是根节点,再看中序遍历HI可得H的左子树为空,右子树是I。
5. 得出二叉树结构
通过上述逐步分析,我们可以构建出如下的二叉树结构:
A |
6. 确定后序遍历结果
后序遍历顺序是“左右根”,按照构建好的二叉树结构,依次访问各子树和节点,就可以得出后序遍历结果为
EDCB IHJGFA。
所以,最终该二叉树的后序遍历结果就是 EDCB IHJGFA 。
Determine \(\Theta\) for the following code fragments in the average case. Assume that all variables are of type int.
sum=0; |
solution : \(\Theta(n)\)
答案解释:
外层循环执行了固定的 3
次,而对于内层循环,每次外层循环迭代时,内层循环都会从
j = 0 到 j = n - 1 执行 n
次。所以总的执行次数就是 3 * n 次。在大 Θ
表示法中,忽略常数系数,只关注与输入规模 n
相关的增长量级,因此这段代码的时间复杂度为 \(\Theta(n)\)。
sum = 0; |
solution : \(\Theta(n^2)\)
答案解释:
外层循环从 i = 1 到 i = n 进行迭代,共执行
n 次。对于每次外层循环的迭代 i,内层循环会从
j = 1 到 j = i 执行 i
次。那么总的执行次数就是:
\[ \begin{align*} &1 + 2 + 3 + \cdots + n\\ =& \frac{n(n + 1)}{2} \end{align*} \]
根据大 Θ 表示法的规则,对于 \(\frac{n(n + 1)}{2}\),其最高次项是 \(n^2\),忽略低阶项和常数系数,所以这段代码的时间复杂度为 \(\Theta(n^2)\)。
sum=0; |
solution : \(\Theta (n)\)
答案解释:
这里根据 n 是否为偶数(通过 EVEN(n)
函数判断)来执行不同的代码块。
如果 n 是偶数,会执行一个 for
循环,该循环从 i = 0 到 i = n - 1 执行
n 次。如果 n 是奇数,则执行
sum = sum + n
这一简单的赋值语句,其执行时间可以看作是常数级别的。
在平均情况下,n
为偶数和奇数的概率大致相等,我们主要关注时间复杂度更高的情况(也就是循环执行的情况)。由于循环执行的次数是与
n 成正比的,所以整体代码的时间复杂度按照大\(\Theta(n)\)表示法来衡量就是\(\Theta(n)\)。
Trace by hand the execution of radix sort algorithm on the array:
int a[] = {265, 301, 751, 129, 937, 863, 742, 694, 76, 438}
答案展示:(注意一下写法)
- initial: 265 301 751 129 937 863 742 694 76 438
- pass 1: [] [301 751] [742] [863] [694] [265] [76] [937] [438] [129]
- pass 2: [301] [] [129] [937 438] [742] [751] [863 265] [76] [] [694]
- pass 3: [76] [129] [265] [301] [438] [] [694] [742 751] [863] [937]
- final sorted array: 76 129 265 301 438 694 742 751 863 937
答案解释:
1. 基数排序(Radix Sort)原理概述
基数排序是一种非比较排序算法,它是按照数字的每一位来进行排序的,对于整数通常从低位到高位依次进行排序,经过多轮排序后最终实现整个数组的有序排列。
2. 具体每轮排序过程解释
Initial(初始状态): 这就是给定的原始数组,数组元素为
{265, 301, 751, 129, 937, 863, 742, 694, 76, 438},此时还未开始进行排序操作。Pass 1(第一轮排序): 在这一轮中,是按照个位数字来对数组元素进行分配。比如个位数字是
1的元素301和751被分到一组(对应上述展示中第二个桶[301 751]);个位数字是2的元素742单独在一个桶里(对应[742]);个位数字是3的元素863在另一个桶(对应[863])等等,依次按照个位数字将所有元素分配到不同的桶中,然后按照桶的顺序依次取出元素,就得到了第一轮排序后的数组状态。Pass 2(第二轮排序): 这一轮是按照十位数字来进行分配。例如十位数字是
0的元素301单独在一个桶(对应[301]);十位数字是2的元素129在一个桶(对应[129]);十位数字是3的元素937和438在一个桶(对应[937 438])等等,同样是将所有元素按十位数字分配到不同桶后,再按桶顺序取出元素,形成第二轮排序后的数组样子。Pass 3(第三轮排序): 本轮依据百位数字来分配元素。像百位数字是
0的元素76在一个桶(对应[76]);百位数字是1的元素129、265、301等分别在相应桶里,按照百位数字的情况把所有元素分配好后,再按顺序取出,经过这一轮排序,数组就已经是有序状态了,得到最终的排序数组{76, 129, 265, 301, 438, 694, 742, 751, 863, 937}。
所以,通过基数排序算法对给定数组进行三轮按照不同数位的分配和整理操作后,最终实现了数组元素的从小到大的有序排列。
Using closed hashing, with double hashing to resolve collisions, insert the following keys into a hash table of eleven slots (the slots are numbered 0 through 10). The hash functions to be used are H1 and H2, defined below. You should show the hash table after all eight keys have been inserted. Be sure to indicate how you are using H1 and H2 to do the hashing. ( The process of your solution is required!!!)
H1(k) = 3k mod 11 H2(k) = 7k mod 10 + 1 Keys: 22, 41, 53, 46, 30, 13, 1, 67.
Answer: H1(22) = 0, H1(41) = 2, H1(53) = 5, H1(46) = 6, no conflict When H1(30) = 2, H2(30) = 1 (2 + 1 _ 1)% 11 = 3,so 30 enters the 3rd slot; H1(13) = 6, H2(13) = 2 (6 + 1 _ 2) % 11 = 8, so 13 enters the 8th slot; H1(1) = 3, H2(1) = 8 (3 + 5 _ 8) % 11 = 10 so 1 enters 10 (pass by 0, 8, 5, 2 ); H1(67) = 3, H2(67) = 10 (3 + 2 _ 10) % 11 = 1 so 67 enters 1 (pass by 2)
答案解释:
1. 闭散列与双散列法原理
- 闭散列(Closed Hashing):也叫开放定址法,是一种解决哈希冲突的方法。当要插入的元素经过哈希函数计算得到的位置已经被占用时,就在哈希表中另外寻找一个空闲的位置来存放该元素,而不是像开散列(链地址法等)那样使用额外的数据结构(如链表)来存储冲突的元素。
- 双散列(Double
Hashing):它是在闭散列基础上用于解决冲突的一种策略。当发生哈希冲突时,使用第二个哈希函数(这里是
H2)来确定探测的步长,通过多次探测(按照一定的规则结合两个哈希函数的结果进行位置计算)来找到合适的空闲位置插入元素。
2. 具体插入各元素的过程及哈希函数使用方式
插入 22: 计算
H1(22),根据哈希函数H1(k) = 3k mod 11,可得H1(22) = 3 * 22 mod 11 = 66 mod 11 = 0,此时哈希表的第 0 个槽位为空,所以直接将 22 插入到第 0 个槽位,没有发生冲突。插入 41: 计算
H1(41),即3 * 41 mod 11 = 123 mod 11 = 2,第 2 个槽位为空,将 41 插入到第 2 个槽位,同样没有冲突。插入 53: 计算
H1(53),3 * 53 mod 11 = 159 mod 11 = 5,第 5 个槽位为空,把 53 插入到第 5 个槽位,无冲突。插入 46: 计算
H1(46),3 * 46 mod 11 = 138 mod 11 = 6,第 6 个槽位此时也是空的,将 46 插入进去,未出现冲突情况。插入 30: 首先计算
H1(30),3 * 30 mod 11 = 90 mod 11 = 2,发现第 2 个槽位已经被 41 占用了,产生了冲突。这时就需要使用双散列来解决冲突,计算H2(30),根据H2(k) = 7k mod 10 + 1,可得H2(30) = 7 * 30 mod 10 + 1 = 210 mod 10 + 1 = 1。然后按照双散列解决冲突的规则,计算新的插入位置,公式为(H1(k) + i * H2(k)) % 表长(这里i表示第i次探测,初始为 1),也就是(2 + 1 * 1) % 11 = 3,第 3 个槽位为空,所以将 30 插入到第 3 个槽位。插入 13: 计算
H1(13),3 * 13 mod 11 = 39 mod 11 = 6,第 6 个槽位已被 46 占用,出现冲突。接着计算H2(13),7 * 13 mod 10 + 1 = 91 mod 10 + 1 = 2。按照冲突解决规则计算新位置,(6 + 1 * 2) % 11 = 8,第 8 个槽位为空,将 13 插入到第 8 个槽位。插入 1: 计算
H1(1),3 * 1 mod 11 = 3,发现第 3 个槽位被 30 占用了,有冲突。计算H2(1),7 * 1 mod 10 + 1 = 8。然后开始按照双散列规则找空闲位置,第一次探测位置是(3 + 1 * 8) % 11 = 10(这里i = 1),第 10 个槽位为空,所以将 1 插入到第 10 个槽位(在这个过程中依次尝试了可能经过的位置,如0、8、5、2等,直到找到空闲的 10 号槽位)。插入 67: 计算
H1(67),3 * 67 mod 11 = 201 mod 11 = 3,第 3 个槽位已被占用,产生冲突。计算H2(67),7 * 67 mod 10 + 1 = 469 mod 10 + 1 = 10。按照冲突解决规则计算新位置,(3 + 1 * 10) % 11 = 1(这里i = 1),发现第 1 个槽位此时为空(在探测过程中经过了 2 号等之前有元素的位置,最终找到空闲的 1 号槽位),所以将 67 插入到第 1 个槽位。
最终得到的哈希表如下(槽位从 0 到 10):
| 槽位编号 | 元素 |
|---|---|
| 0 | 22 |
| 1 | 67 |
| 2 | 41 |
| 3 | 30 |
| 4 | |
| 5 | 53 |
| 6 | 46 |
| 7 | |
| 8 | 13 |
| 9 | |
| 10 | 1 |
通过这样使用 H1 和 H2
这两个哈希函数以及双散列解决冲突的方法,成功将所有给定的键插入到了哈希表中。
You are given a series of records whose keys are integers. The records arrive in the following order: C, S, D, T, A, M, P, I, B, W, N, G, U, R. Show the 2-3 tree that results from inserting these records. (the process of your solution is required!!!)
答案展示:
以下是逐步构建 2 - 3 树的过程:
- 插入
C:
[C] |
- 插入
S:
[C, S] |
- 插入
D:
[D] |
- 插入
T:
[D] |
- 插入
A:
[D] |
- 插入
M:
[D, S] |
- 插入
P:
[D, S] |
- 插入
I:
[M] |
- 插入
B:
[M] |
- 插入
W:
[M] |
- 插入
N:
[M] |
- 插入
G:
[M] |
- 插入
U:
[M] |
- 插入
R:
[M, S] |
答案解释:
1. 2 - 3 树的基本性质
2 - 3 树是一种自平衡的多路查找树,它有以下特点:
- 每个节点可以包含 1 个或 2 个键值(对应 2 个或 3 个子树)。
- 所有叶子节点都在同一层,保证了树的平衡性,使得查找、插入、删除等操作的时间复杂度相对稳定。
2. 插入操作及节点处理原则
- 插入过程: 从根节点开始,根据键值的大小比较来决定沿着哪条路径向下查找合适的插入位置。当找到对应的叶子节点时,将键值插入到该节点中。
- 节点溢出处理: 如果插入后节点的键值个数超过了 2 个(达到 3 个),就需要进行分裂操作。将节点中的中间键值提升到父节点(如果父节点不存在,则创建一个新的父节点),原节点中小于中间键值的键值组成左子树,大于中间键值的键值组成右子树,以此来保持 2 - 3 树的结构特性,保证树的平衡性以及符合其节点键值数量的要求。
通过按照上述规则依次插入给定的各个记录,就逐步构建出了最终的 2 - 3 树结构。
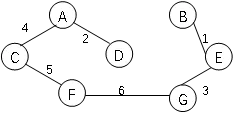
Use Dijkstra’s Algorithm to find the shortest paths from C to all other vertices.
答案:C to A: 4 (C,A); CF: 5(C,F); CD: 6(C,A,D); CB: 12(C,A,D,B); CG:11 (C,F,G); CE: 13(C,A,D,B,E)
Use Kruskal’s algorithm to find the minimum-cost spanning tree.
答案:
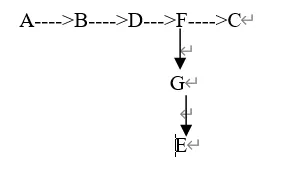
Show the DFS tree for the following graph, starting at Vertex A.
答案: